Maths Standard Term 2 Sample Paper 2022 (Solved)

Class 10 Maths Standard Term 2 Sample Paper 2022, (Maths) exams are Students are taught thru NCERT books in some of the state board and CBSE Schools. As the chapter involves an end, there is an exercise provided to assist students to prepare for evaluation. Students need to clear up those exercises very well because the questions inside the very last asked from those.

Sometimes, students get stuck inside the exercises and are not able to clear up all of the questions. To assist students, solve all of the questions, and maintain their studies without a doubt, we have provided a step-by-step NCERT Sample Question Papers for the students for all classes. These answers will similarly help students in scoring better marks with the assist of properly illustrated Notes as a way to similarly assist the students and answer the questions right.

General Instructions :

1. The question paper consists of 14 questions divided into 3 sections A , B , C.

2. All questions are compulsory .

3. Section A comprises of 6 questions of 2 marks each . Internal choice has been provided in two questions

4. Section B comprises of 4 questions of 3 marks each . Internal choice has been provided in one question.

5. Section C comprises of 4 questions of 4 marks each . An internal choice has been provided in one question. It contains two case study based questions .

Section – A

[ 2 Marks Each ]

1. Find the 20^th term from the last term of the A.P.: 3 , 8 , 13 , ….. 253 .

OR

If 7 times the 7^th term of an A.P. is equal to 11 times its 11^th term , then find its 18^th term .

2. A fast train takes 3 hours less than a slow train for a journey of 600 km . If the speed of the slow train is 10 km / h less than that of the fast train , find the speed of each train .

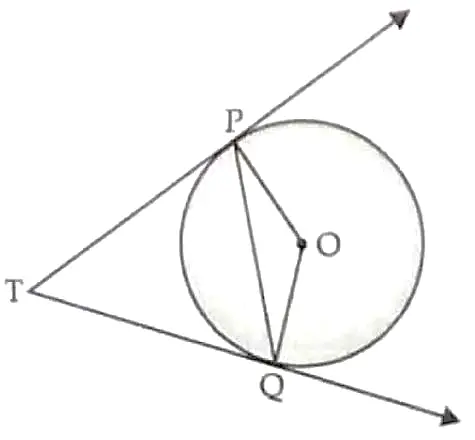
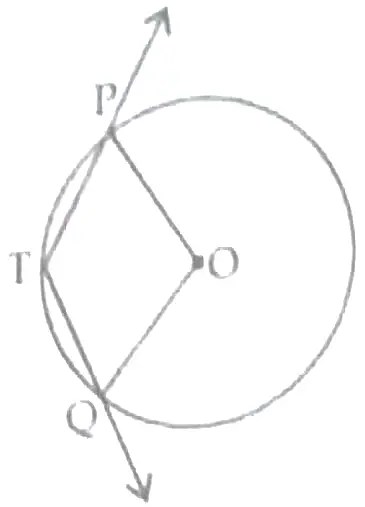
3. In the given figure PQ is chord of length 6 cm of the circle of radius 6 cm . TP and TQ are tangents to the circle at points P and Q respectively . Find ∠PTQ.

4. A well of diameter 4 m dug 21 m deep . The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 3 m to form an embankment . Find the height of the embankment

5. Find the mode of the following frequency distribution :

6. For what values of k , the roots of the equation x² + 4x + k = 0 are real ?

OR

Find the nature of roots of the quadratic equation 2x² – 4x + 3 = 0 .

Section – B

[ 3 Marks Each ]

7. The table below show the salaries of 280 persons :

Calculate the median salary of the data .

8. Draw two tangents to a circle of radius 4 cm , which are inclined to each other at an angle of 60 ° .

9. Daily wages of 110 workers , obtained in a survey , are tabulated below :

Compute the mean daily wages of these workers .

10. Two poles of equal heights are standing opposite to each other on either side of the road which is 80 m wide . From a point in between them on the road , the angles of elevation of the top of poles are 60 ° and 30 ° respectively . Find the height of the poles and the distances of the point P from the poles .

OR

From a point P on the ground , the angle of elevation of the top of a tower is 30 ° and that of the top of the flag – staff fixed on the top of the tower is 45 ° . If the length of the flag – staff is 5 m , find the height of the tower . ( Use √3 = 1.732 )

Section – C

[ 4 Marks Each ]

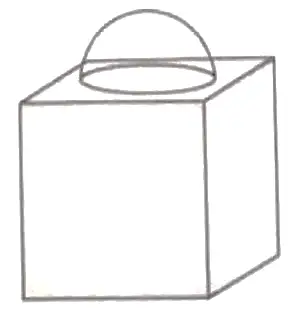
11. The given figure is a decorative block , made up of two solids : a cube and a hemisphere . The base of the block is a cube of side 6 cm and the hemisphere fixed on the top has a diameter of 3.5 cm . Find the total surface area of the block . [ Use π = 22/7 ] .

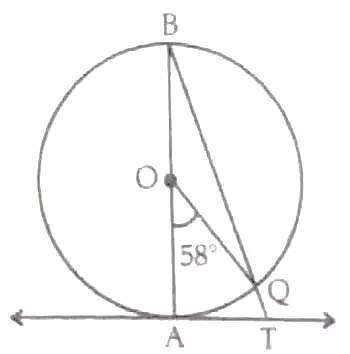
12. In given figure , AB is the diameter of a circle with centre O and AT is a tangent . If ∠AOQ = 58° , find ∠ATQ .

OR

Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle .

Case Study – 1

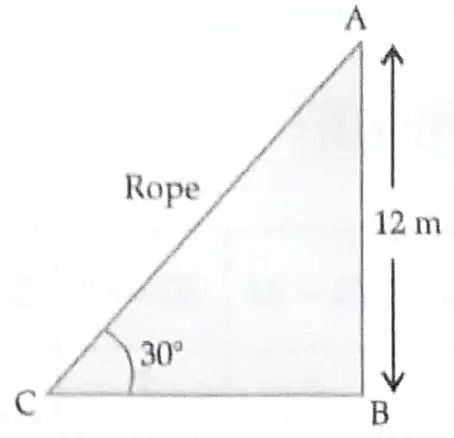
13. A circus artist is climbing from the ground along a rope stretched from the top of a vertical pole and tied at the ground . The height of the pole is 12 m and the angle made by the rope with ground level is 30 ° .

Give answer of the following questions :

( i ) Find the distance covered by the artist in climbing the top of the pole .         [ 2 ]

( ii ) Calculate the length of BC .         [ 2 ]

Case Study – 2

14. Jaspal Singh takes a loan from a bank for his car .

Jaspal Singh repays his total loan of ₹ 118000 by paying every month starting with the first installment of ₹ 1000. If he increases the installment by ₹ 100 every month .

( i ) Calculate the amount paid by him in 25^th installment .           [ 2 ]

( ii ) Calculate the amount paid by him in 30^th installment .           [ 2 ]

Solution of Sample Paper

Section – A

1. 20^th term from the end = 1 – ( n – 1 ) d            ½

= 253 – 19 x 5           1

= 158         ½

Detailed Solution :

Given , A.P .: 3 , 8 , 13 , ……….. 253

Here , first term ( a ) = 3 , common difference ( d ) = 8 – 3 = 5 and last term ( l ) = 253           1

Then , 20^th term from the end of the A.P.

= l – ( n – 1 ) d

= 253 – ( 20 – 1 ) 5

= 253 – 95

= 158               1

OR

7a₇ = 11a₁₁

⇒ 7 (a + 6d ) = 11 ( a + 10d )           1

⇒ a + 17d = 0

∴ a₁₈ = 0           1

Detailed Solution :

Given , 7a₇ = 11a₁₁

∴ a_n = a + ( n – 1 ) d

Then , 7 [ a + ( 7 – 1 ) d ] = 11 [ a + ( 11 – 1 ) d ]

⇒ 7 ( a + 6d ) = 11 ( a + 10d )

⇒ 7a + 42d = 11a + 110 d

⇒ 11a – 7a = 42d – 110d

⇒ 4a = -68d

⇒ a = -17d            1

⇒ a + 17d = 0

i.e., a + ( 18 – 1 ) d = 0

Hence , a₁₈ = 0 .           1

2. Total distance of the journey = 600 km

Let speed of fast train = x km / h ,

then speed of slow train = ( x – 10 ) km / h

According to question ,

Either , x = 50 or x = -40

∴ speed can not be negative .

So , the speed of fast train = 50 km / h ,

and the speed of slow train = 50 – 10 = 40 km / h .           1

3. Here , PQ = 6 cm , OP = OQ = 6 cm ( radii )

∴ PQ = OP = OQ

∠POQ = 60 ° ( angle of equilateral △ )              ½

∠OPT = ∠OQT = 90 ° ( radius ⊥ tangent )

∴ ∠PTQ + 90 ° + 90 ° + 60 ° = 360 ° ( angle sum property )         ½

∠PTQ = 120 °         1

4. Diameter of well = 4 m

Radius of well , r = 2 m

Depth of well , h = 21 m ,

Volume of earth dug out = πr²h

22 / 7 x 2 x 2 x 21

= 264 m³                 ½

Width of embankment = 3 m

Outer radius of ring = 2 + 3 = 5 m

Let the height of embankment be h

∴ Volume of embankment = Volume of earth dug out

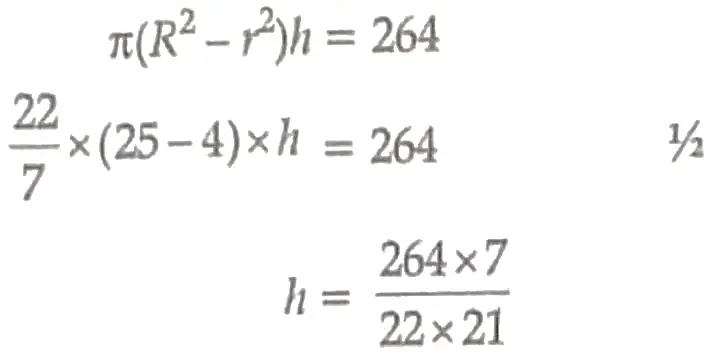
∴ Height of embankment = 4 m .          1

5. Modal class is 30-40

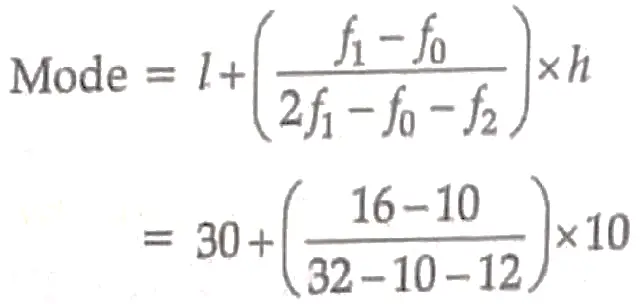
= 36.              2

Detailed Solution :

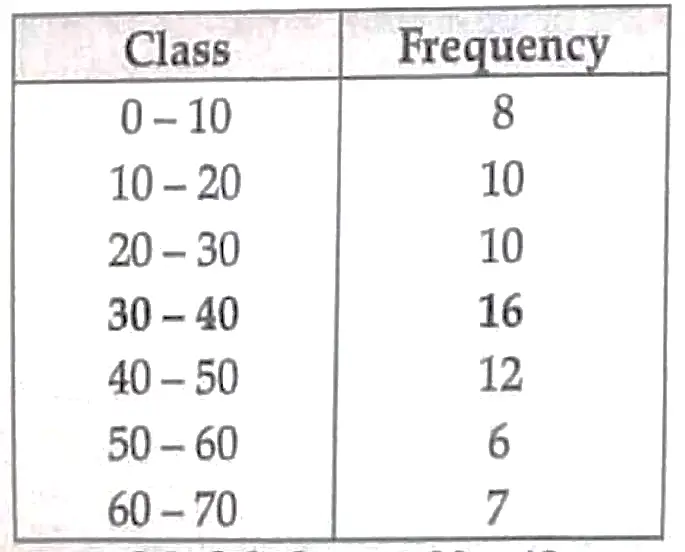
Modal – class = 30 – 40

⇒ l = 30 , f₀ = 10 , f₁ = 16 , f₂ = 12 , h = 10

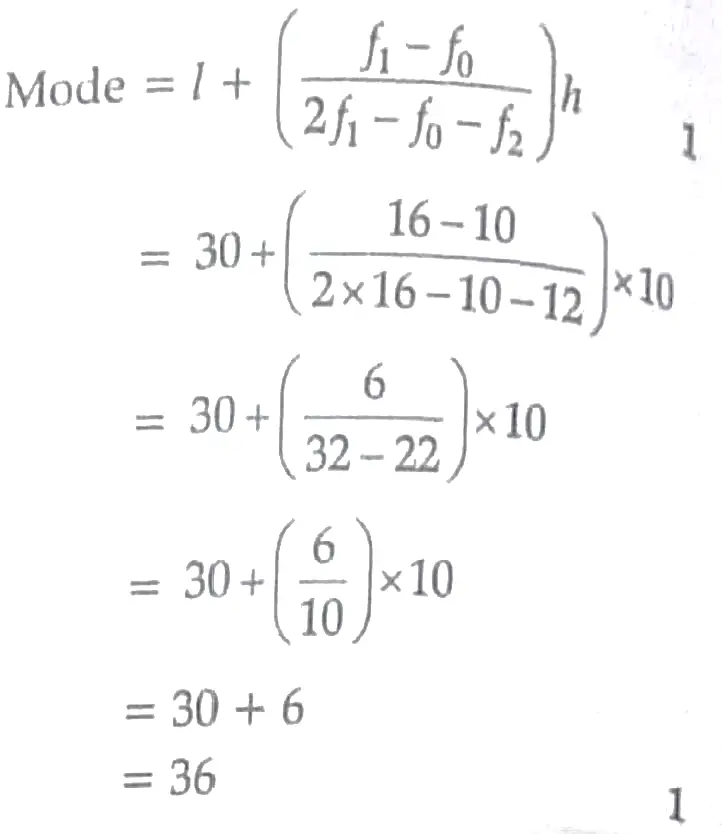
6. Since roots of the equation x² + 4x + k = 0 are real

⇒ 16 – 4k ≥ 0

⇒ k ≤ 4             2

Detailed Solution :

Given x² + 4x + k = 0 .

Comparing the given equation with

ax² + bx + c = 0 ,

we get a = 1 , b = 4 , c = k             1

Since , given the equation has real roots

⇒ D ≥ 0

⇒ b² – 4ac ≥ 0

⇒ 4² – 4 × 1 × k ≥ 0

⇒ 4k ≤ 16

⇒ k ≤ 4         1

OR

Given : 2x² – 4x + 3 = 0

On comparing above with ax² + bx + c = 0 ,

we get , a = 2 , b = -4 , c = 3         1

Now , D = b² – 4ac

So , D = ( -4 ) ² – 4 ( 2 ) × ( 3 )

= -8 < 0 or ( -ve )

Hence , the given equation has no real roots .          1

Section – B

7.

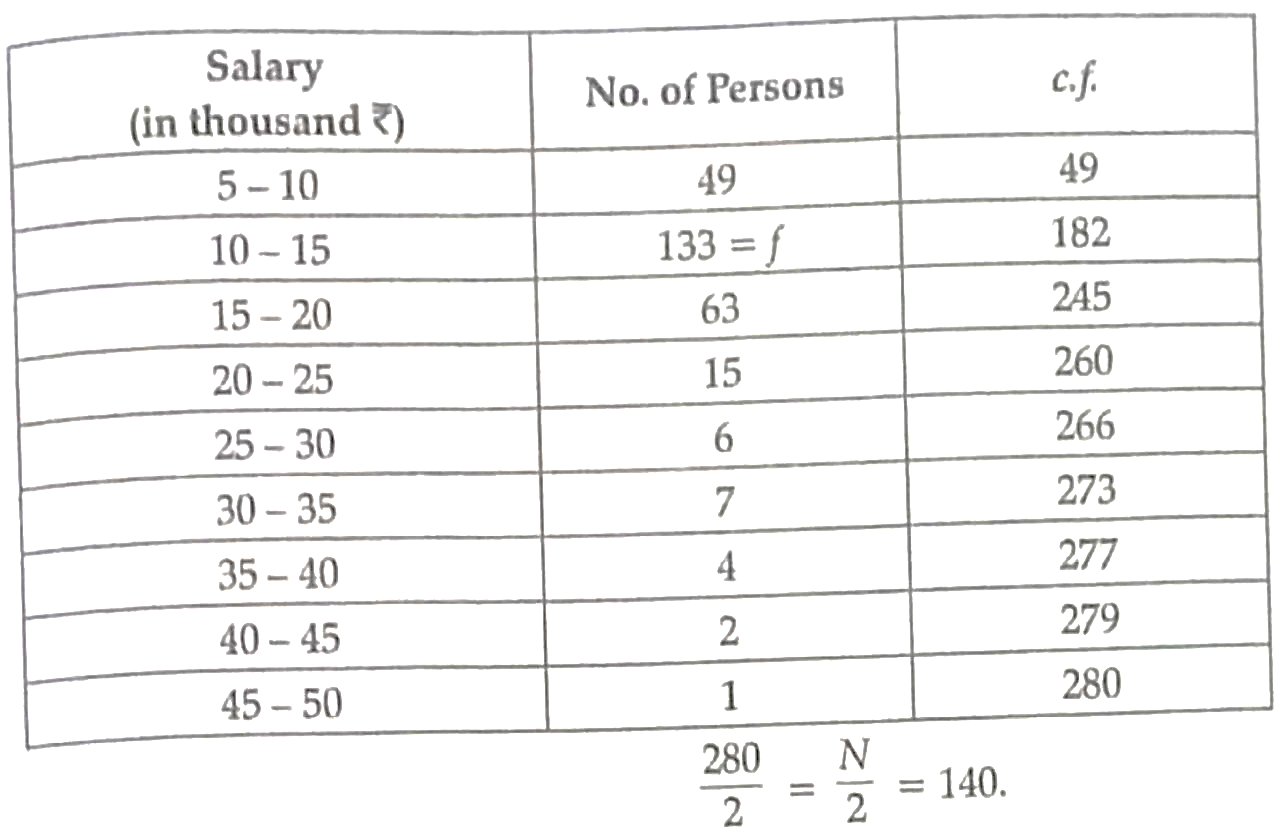                       1

Median class = 10 – 15 .

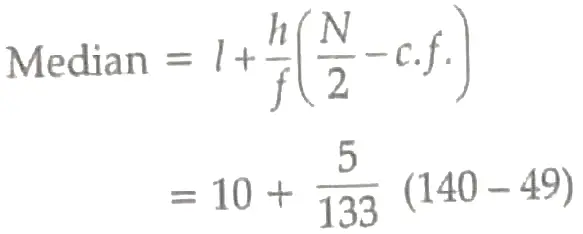                    1

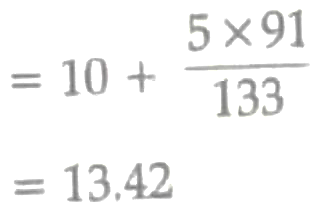
Hence , median salary is ₹ 13.42 thousand or ₹ 13420 ( approx ) .           1

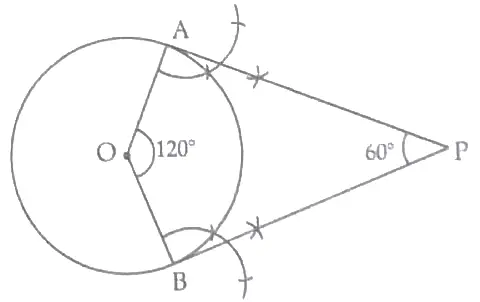
8. Steps of construction :              1

( i ) Draw a circle of radius 4 cm with O as centre .

( ii ) Draw two radii OA and OB inclined to each other at an angle of 120 ° .

( iii ) Draw AP ⊥ OA at A and BP ⊥ OB at B. Which meet at P.

( iv ) PA and PB are the required tangents inclined to each other an angle of 60 ° .

           2

9.

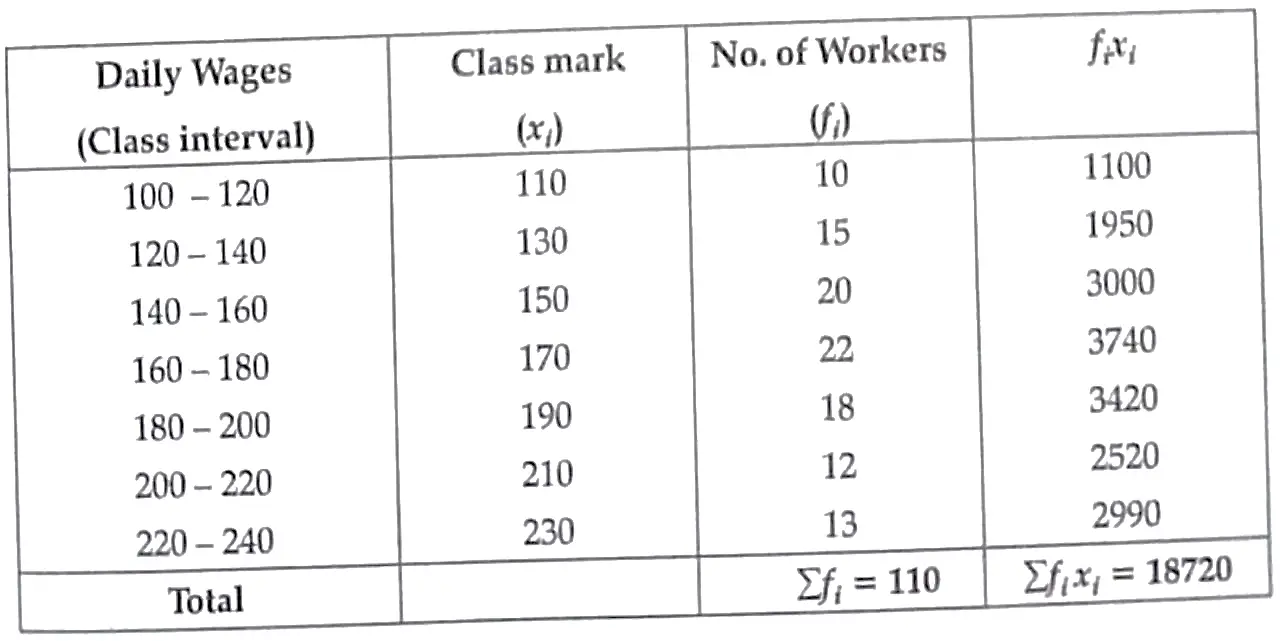              1½

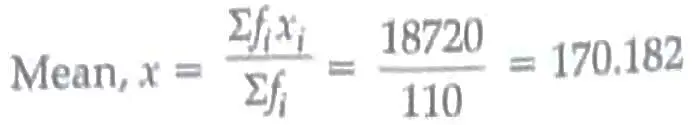
Hence , mean daily : wages are ₹ 170.182 ( Approx.)            ½

10. Let two poles be AB and CD ,

then AB = CD = h

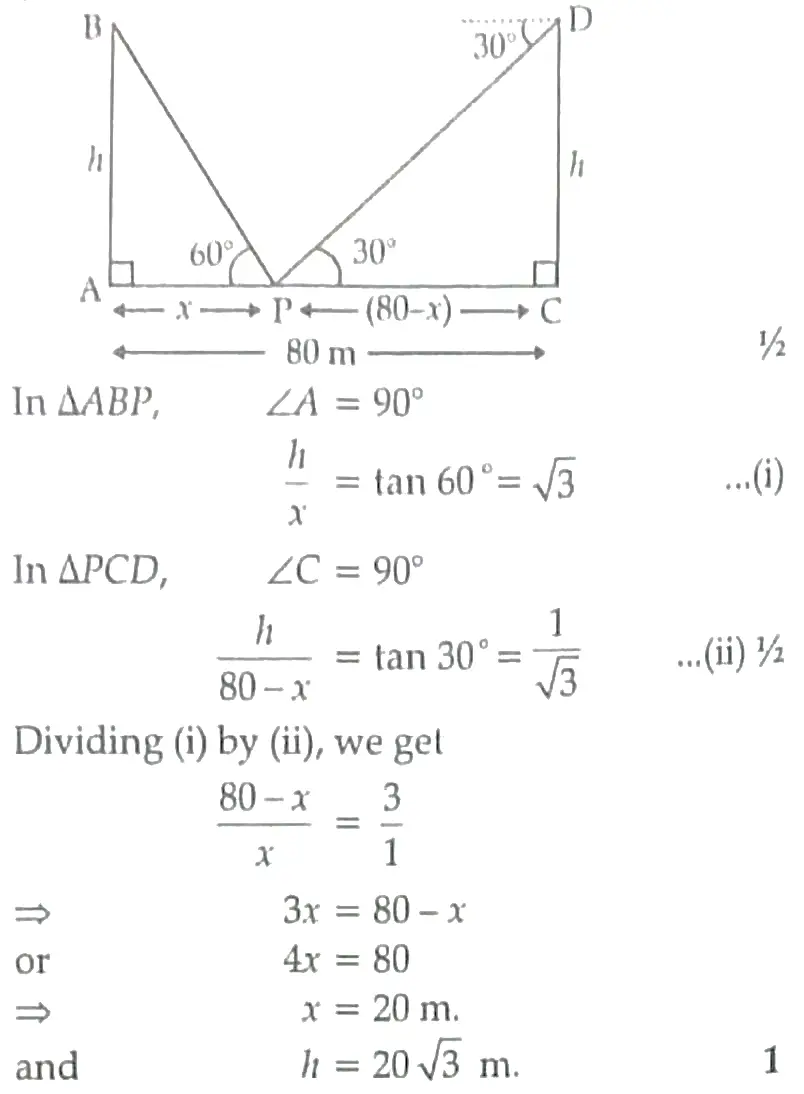
∴ Height of poles is 20 √3 m

and the distances of P are 20 m and 60 m from poles .              ½

OR

Let AB be a tower and BC be a flagstaff .

According to question ,

In △PAC , ∠A = 90 °

AC / AP = tan 45 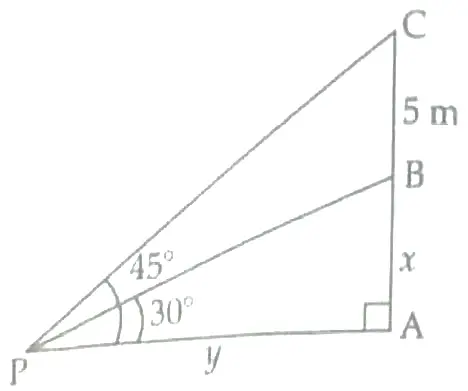° = 1

             ½

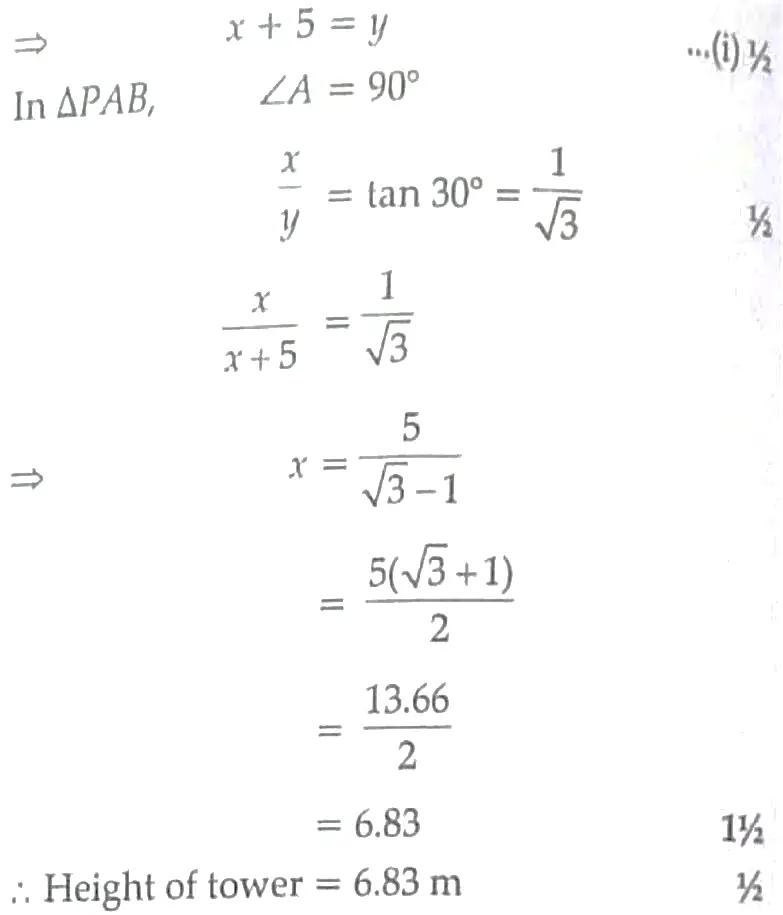
Section – C

11. Surface area of block

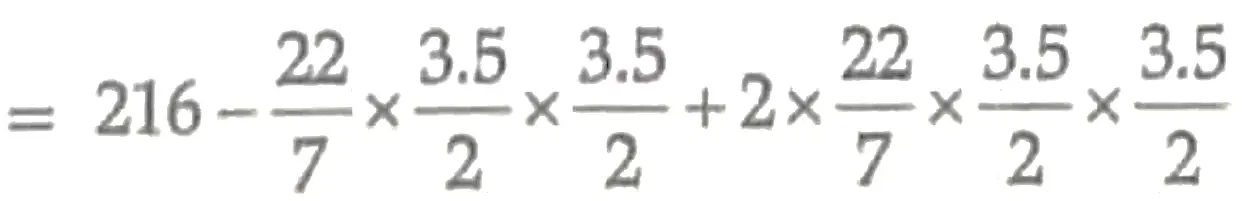            1½ + 1½

= 225.625 cm² .               1

Detailed Solution :

Given , Side of cube = 6 cm

Diameter of hemisphere = 3.5 cm

Radius of hemisphere = 3.5 / 2         ½

Total surface area of cube = 6a²

= 6 x ( 6 ) ² = 216 cm²                  ½

Total surface area of solid = TSA of cube – Area of circle + CSA of hemisphere .

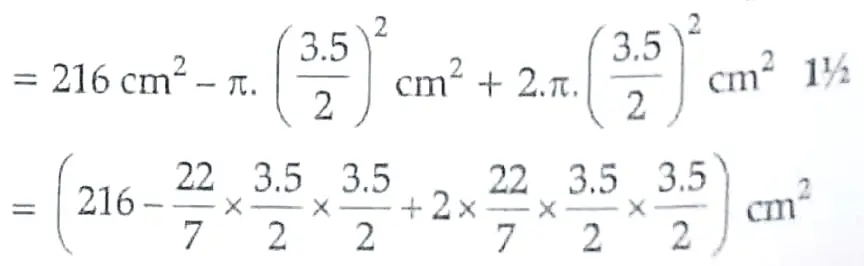
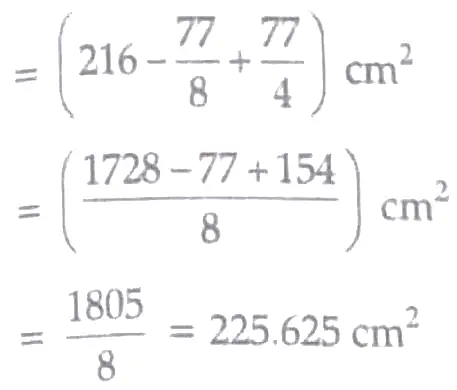              1½

12 . ∠AOQ = 58 ° ( Given )

∠ABQ = = 1/2 ∠AOQ     ( Angle on the circumference of the circle by the same arc )           1½ 

= 1 / 2 x 58 °

= 29 °            1

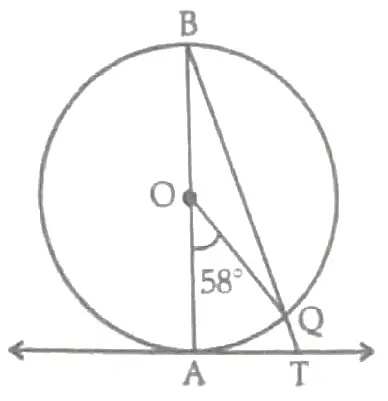
∠BAT = 90 ° ( ∴ OA ⊥ AT )

∠ATQ = 90 ° – 29 °

= 61 °          1½

OR

Given : A circle with centre O is inscribed in a quadrilateral ABCD .

In △AEO and △AFO ,

OE = OF ( radii of circle )

∠OEA = ∠OFA = 90 ° ( radius is ⊥ to tangent 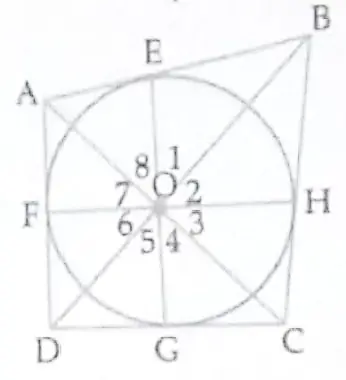)              ½

           ½

The point of contact is perpendicular to the tangent .

OA = OA ( common side )

△AEO ≅ △AFO ( R.H.S. congruency )

∠7 = ∠8 ( By cpct )        ……( i )              1½

Similarly ,

∠1 = ∠2    …..( ii )

∠3 = ∠4    ..…( iii )

∠5 = ∠6    …..( iv )

∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360 °   ( angle around a point is 360 ° )        ½ 

2∠1 + 2∠8 + 2∠4 + 2∠5 = 360 °

∠1 + ∠8 + ∠4 + ∠5 = 180 °

( ∠1 + ∠8 ) + ( ∠4 + ∠5 ) = 180 °             1

∠AOB + ∠COD = 180 °

Hence Proved .

Case Study – 1

13. ( i ) Clearly , distance covered by the artist is equal to the length of the rope AC .

Let AB be the vertical pole of height 12 m .

It is given that ∠ACB = 30 °

Thus , in right – angled triangle ABC ,         1

sin 30 ° = AB / AC

⇒ 1 / 2 = 12 / AC

∴ AC = 24 m .            1

( ii ) In △ ABC , ∠B = 90 °

tan 30 ° = AB / BC

⇒ 1 / √3 = 12 / BC

⇒ BC = 12√3 m .          2

Case Study – 2

14. ( i ) The amount paid by him in 25^th installment is :

T₂₅ = a + 24d                  1

= 1000 + 24 × 100

= 1000 + 2400

= ₹ 3400 .               1

( ii ) The amount paid by him in 30^th installment ,

T₃₀ = a + 29d             1

= 1000 + 29 x 100

= 1000 + 2900

= ₹ 3900 .            1