Maths Standard Term 2 Sample Paper 2022 (Solved)

Class 10 Maths Standard Term 2 Sample Paper 2022, (Maths) exams are Students are taught thru NCERT books in some of the state board and CBSE Schools. As the chapter involves an end, there is an exercise provided to assist students to prepare for evaluation. Students need to clear up those exercises very well because the questions inside the very last asked from those.

Sometimes, students get stuck inside the exercises and are not able to clear up all of the questions. To assist students, solve all of the questions, and maintain their studies without a doubt, we have provided a step-by-step NCERT Sample Question Papers for the students for all classes. These answers will similarly help students in scoring better marks with the assist of properly illustrated Notes as a way to similarly assist the students and answer the questions right.

Class 10 Maths Standard Term 2 Sample Paper 2022

General Instructions :

1. The question paper consists of 14 questions divided into 3 sections A , B , C.

2. All questions are compulsory .

3. Section A comprises of 6 questions of 2 marks each . Internal choice has been provided in two questions

4. Section B comprises of 4 questions of 3 marks each . Internal choice has been provided in one question.

5. Section C comprises of 4 questions of 4 marks each . An internal choice has been provided in one question. It contains two case study based questions .

Section – A

[ 2 Marks Each ]

1. How many two digits numbers are divisible by 3?

OR

Find the number of natural numbers between 102 and 998 which are divisible by 2 and 5 both .

2. Solve the following quadratic equation for x :

9x² – 9 ( a + b ) x + 2a² + 5ab + 2b² = 0

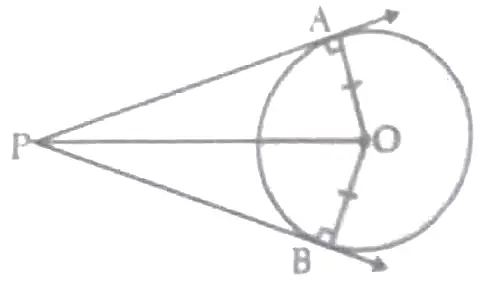
3. Prove that the lengths of two tangents drawn from an external point to a circle are equal .

4. The volume of a right circular cylinder with its height equal to the radius , is 25 1/7 cm³ . Find the height 7 of the cylinder ( Use π = 22/7 )

5. Given below is the distribution of weekly pocket money received by students of a class . Calculate the pocket money that is received by most of the students .

6. For what value ( s ) of ‘ a ‘ quadratic equation 3ax² – 6x + 1 = 0 has no real roots ?

OR

If one root of the equation ( k – 1 )x² – 10x + 3 = 0 is the reciprocal of the other , then find the value of k.

Section – B

[ 3 Marks Each ]

7. On annual day of a school , 400 students participated in the function . Frequency distribution showing their ages is as shown in the following table :

Find mean and median of the above data .

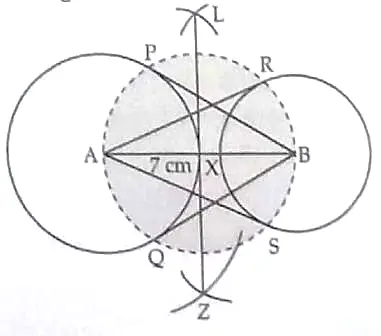
8. Draw a line segment AB of length 7 cm . Taking A as centre , draw a circle of radius 3 cm and taking B as centre , draw another circle of radius 2 cm . Construct tangents to each circle from the centre of the other circle .

9. The mean of the following distribution is 53. Find the missing frequency k ?

10. Two points A and B are on the same side of a tower and in the same straight line with its base . The angle of depression of these points from the top of the tower are 60 ° and 45 ° respectively . If the height of the tower is 15 m , then find the distance between these points .

OR

A moving boat observed from the top of a 150 m high cliff , moving away from the cliff . The angle of depression of the boat changes from 60 ° to 45 ° in 2 minutes . Find the speed of the boat .

Section – C

[ 4 Marks Each ]

11. A wooden article was made by scooping out a hemisphere from each end of a solid cylinder , as shown in fig . If the height of the cylinder is 10 cm and its base is of radius 3.5 cm . Find the total surface area of the article .

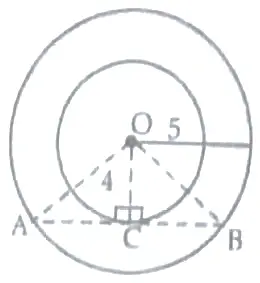
12. If the radii of two concentric circles are 4 cm and 5 cm , then find the length of each chord of one circle which is tangent to the other circle .

OR

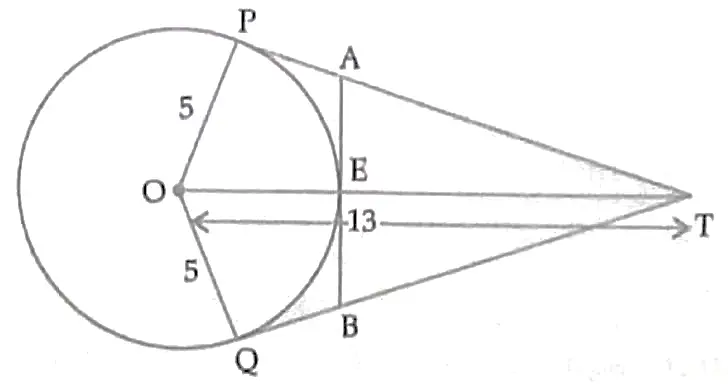
In Fig . O is the centre of a circle of radius 5 cm . T is a point such that OT = 13 cm and OT intersects circle at E. If AB is a tangent to the circle at E , find the length of AB , where TP and TQ are two tangents to the circle .

Case Study – 1

13. A group of students of class X visited India Gate on an education trip . The teacher and students had interest in history as well . The teacher narrated that India Gate , official name Delhi Memorial , originally called All – India War Memorial , monumental sandstone arch in New Delhi , dedicated to the troops of British India who died in wars fought between 1914 and 1919. The teacher also said that India Gate , which is located at the eastern end of the Rajpath ( formerly called the Kings way ) , is about 138 feet ( 42 metres ) in height .

( i ) What is the angle of elevation if they are standing at a distance of 42 m away from the monument ?          [ 2 ]

( ii ) They want to see the tower at an angle of 60 ° . So , they want to know the distance where they should stand and hence find the distance .          [ 2 ]

Case Study – 2

14. Your friend Veer wants to participate in a 200 m race . He can currently run that distance in 51 seconds and with each day of practice it takes him 2 seconds less . He wants to do in 31 seconds .

( i ) Write in AP for the given situation .         [ 2 ]

( ii ) What is the minimum number of days he needs to practice till his goal is achieved ?         [ 2 ]

Solution of Sample Paper

Section – A

1. Lowest two digit number divisible by 3 is 12 .

and highest two digit number divisible by 3 is 99 .

Hence , the sequence start with 12 and ends with 99 and common difference is 3 .

So , the A.P. will be 12 , 15 , 18 , —- , 96 , 99

Here , a = 12 , d = 3 , l = 99

∴ l = a + ( n − 1 ) d         1

∴ 99 = 12 + ( n – 1 ) 3

⇒ 99 – 12 = 3 ( n – 1 )

⇒ n – 1 = 87 / 3

⇒ n – 1 = 29

⇒ n = 30

Therefore , there are 30 , two digit numbers which are divisible by 3 .         1

OR

The number which ends with 0 is divisible by 2 and 5 both .

∴ Such numbers between 102 and 998 are :

110 , 120 , 130 , ……., 990 .

Last term , a_n = 990

a + ( n + 1 ) d = 990          1

110 + ( n – 1 ) x 10 = 990 (∴ a = first term = 110 )

110 + 10n – 10 = 990

10n + 100 = 990

10n = 990 – 100

10n = 890

n = 890 / 10 = 89 .            1

2. Given ,

9x² – 9 ( a + b ) x + 2a² + 5ab + 26² = 0

First , we solve ,

2a² + 5ab + 2b² = 2a² + 4ab + ab + 2b²

Here , = 2a [ a + 2b ] + b [a + 2b ]

= ( a + 2b ) ( 2a + b )           ½

Hence , the equation becomes

9x² − 9 ( a + b ) x + ( a + 2b ) ( 2a + b ) = 0

⇒ 9x² – 3 [ 3a + 3b ] x + ( a + 2b ) ( 2a + b ) = 0

⇒ 9x² – 3 [ ( a + 2b ) + ( 2a + b ) ] x + ( a + 2b ) ( 2a + b ) = 0

⇒ 9x² – 3 ( a + 2b ) x – 3 ( 2a + b ) x + ( a + 2b ) ( 2a + b ) = 0

⇒ 3x [ 3x- ( a + 2b ) ] − ( 2a + b ) [ 3x – ( a + 2b ) ] = 0

⇒ [ 3x – ( a + 2b ) ] [ 3x – ( 2a + b ) ] = 0             ½

⇒ 3x – ( a + 2b ) = 0 or 3x – ( 2a + b ) = 0

⇒ x = a + 2b / 3 or x = 2a + b / 3             ½

Hence , the roots = a + 2b / 3 , 2a + b / 3            ½

3. Given , AP and BP are tangents of circle having centre O.

             ½

To Prove : AP = BP

Construction : Join OP , AO and BO

36 = 2a² + ab + ab + 26² 2a [ a + 2b ] + b [ a + 2b ]              ½

Proof : In △OAP and △OBP

OA = OB ( Radius of circle )

OP = OP ( Common side )

∠OAP = ∠OBP = 90 ° ( Radius ⊥ tangent )

△OAP ≅ △OBP ( RHS congruency rule )

AP = BP ( By cpct )            1

Hence Proved .

4. Given ,

5 .

= 86.31 ( approx . )

Hence , mode = 86.31 .            1

6. Given that,

3ax² – 6x + 1 = 0

For no real roots b² – 4ac < 0             1

Discriminant D < 0 so ,

( -6 ) ² – 4 ( 3a ) ( 1 ) < 0

12a > 36

a > 3           1

Detailed Solution :

Given , 3ax² – 6x + 1 = 0

On Comparing with AX² + BX + C = 0 ,

we get A = 3a , B = -6 and C = 1

Discriminant , D = B² – 4AC

= ( – 6 ) ² – 4 × 3a × 1

= 36 – 12a         1

For condition of ‘ no real roots ‘ ,

B² – 4AC < 0

⇒ 36 – 12a < 0

⇒ 12a > 36

⇒ a > 3 .            1

OR

Let one root = α

and the other root = 1 / α

Product of roots = α x 1 / α = 1            1

Given equation , ( k – 1 ) x² – 10x + 3 = 0

Comparing it with standard quadratic equation

ax² + bx + c = 0

we get , a = ( k – 1 ) , b = – 10 & c = 3

Product of roots = c / a = 3 / ( k – 1 )

1 = 3 / ( k – 1 )

or , 3 = k – 1

or , k = 4 .          1

Section – B

7 .

8. Steps of construction :

( i ) Draw a line segment AB = 7 cm .

( ii ) With A as centre and radius 3 cm draw a circle .

( iii ) With B as centre and radius 2 cm draw another circle .

( iv ) Taking AB as diameter and draw perpendicular bisector , which intersects first two circles at P and Q , R and S.         1

( v ) Join B to P and Q , A to R and S.

Hence , BP , BQ , AR and AS are the required tangents .              1

            1

9 .

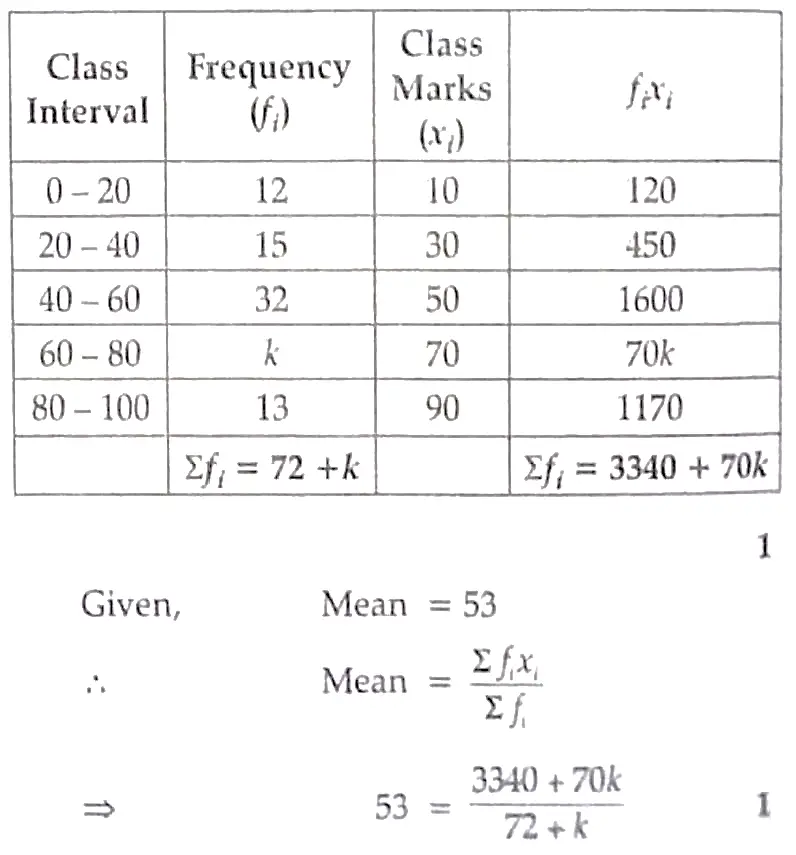
⇒ 53 ( 72 + k ) = 3340 + 70k

⇒ 3816 + 53k = 3340 + 70k

⇒ 70k – 53k = 3816 – 3340

⇒ 17k = 476

⇒ k = 28

Hence , value of k is 28 .          1

10. Let the distance between these points be y m . Also , let CA be x m .

OR

Section – C

11. Total surface Area of article

= CSA of cylinder + CSA of 2 hemispheres

CSA of cylinder = 2πrh         ½

= 2 x 22/7 x 3.5 x 10

= 220 cm²       1

Surface area of two hemispherical scoops = 4πr²        ½

= 4 x 22/7 x 3.5 x 3.5

= 154 cm²         1

∴ Total surface area of article = 220 + 154

= 374 cm²         1

12. Here , radii of two concentric circles ,

OC = 4 cm and

OB = 5 cm

In right angled △OBC , ∠C = 90 °

CO² + BC² = OB² ( Using Pythagoras theorem )           1

4² + BC² = 5²

16+ BC² = 25

BC² = 25 – 16

BC² = 9

BC = 3 cm           ½

            1

Since , AB is the chord and OC ⊥ AB , that divides AB in two equal parts

Hence , AB = 2 x BC

= 2 x 3

= 6 cm

OR

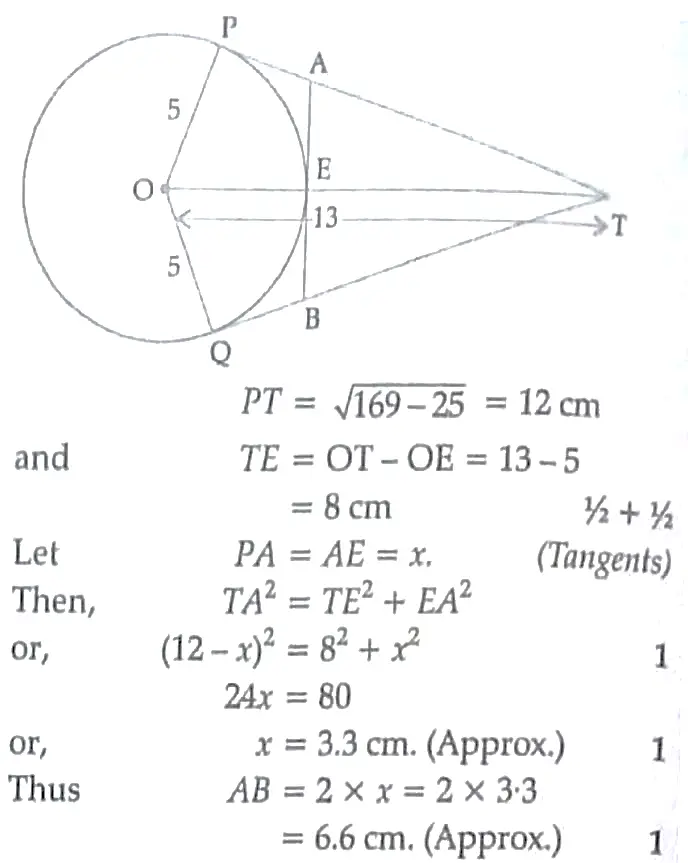
Case Study – 1

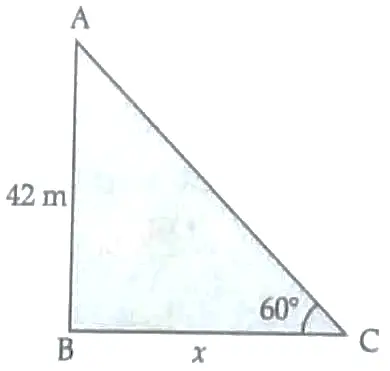
13. ( i ) Height of India gate = 42 m

Distance between students and Indian gate = 42 m

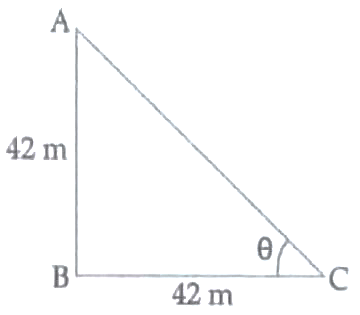
Now , △ABC , ∠B = 90 °

tan θ = AB / BC           1

tan θ = 42 / 42

tan θ = 1

tan θ = tan 45 °

θ = 45 °

Hence , angle of elevation = 45 ° .          1

( ii ) Height of India gate = 42 m

Angle = 60 °

Let the distance between students and India gate = x m .

              1

Now , In △ABC , ∠B = 90 °

tan θ = AB / BC

tan 60 ° = 42 / x

√3 = 42 / x

x = 42 / √3

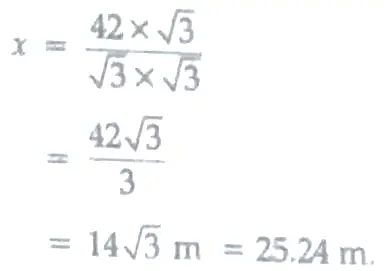             1

Case Study – 2

14. ( i ) a = 51

d = -2

For an AP , the common difference of each term will be same .

First term ( a ) = 51 seconds

Common difference ( d ) = 2 seconds

AP = 51 , 49 , 47 …….          2

( ii ) Goal = 31 second

n = number of days

∴ a_n = 31

a + ( n – 1 ) d = 31

51 + ( n – 1 ) ( – 2 ) = 31

51 – 2n + 2 = 31

-2n = 31 – 53

-2n = -22

n = 11 .                2