Maths Standard Term 2 Sample Paper 2022 (Solved)

Class 10 Maths Standard Term 2 Sample Paper 2022, (Maths) exams are Students are taught thru NCERT books in some of the state board and CBSE Schools. As the chapter involves an end, there is an exercise provided to assist students to prepare for evaluation. Students need to clear up those exercises very well because the questions inside the very last asked from those.

Sometimes, students get stuck inside the exercises and are not able to clear up all of the questions. To assist students, solve all of the questions, and maintain their studies without a doubt, we have provided a step-by-step NCERT Sample Question Papers for the students for all classes. These answers will similarly help students in scoring better marks with the assist of properly illustrated Notes as a way to similarly assist the students and answer the questions right.

Class 10 Maths Standard Term 2 Sample Paper 2022

General Instructions :

1. The question paper consists of 14 questions divided into 3 sections A , B , C.

2. All questions are compulsory .

3. Section A comprises of 6 questions of 2 marks each . Internal choice has been provided in two questions

4. Section B comprises of 4 questions of 3 marks each . Internal choice has been provided in one question.

5. Section C comprises of 4 questions of 4 marks each . An internal choice has been provided in one question. It contains two case study based questions .

Section – A

[ 2 Marks Each ]

1. Which term of the A.P. 27 , 24 , 21 , ……. is zero ?

OR

In an Arithmetic Progression , if d = -4 , n = 7 , a = 4 , then find a .

2. Find the roots of the equation x² + 7x + 10 = 0 by using quadratic formula .

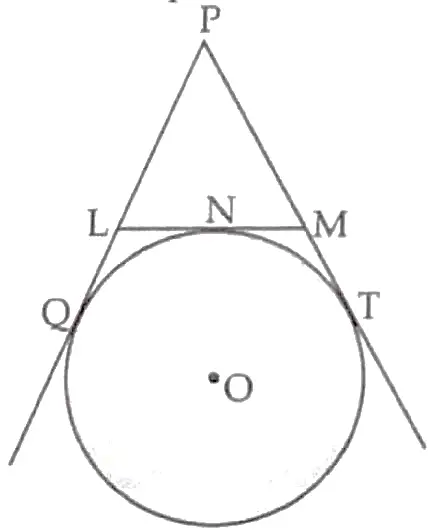
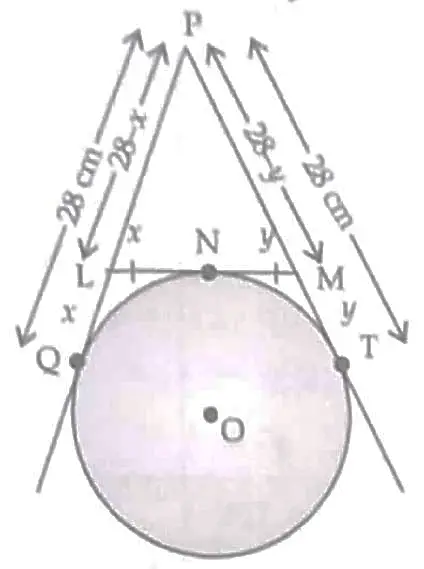
3. In the following , if PQ = 28 cm , then find the perimeter of △PLM .

4. From a solid right circular cylinder of height 14 cm and base radius 6 cm , a right circular cone of same height and same base removed . Find the volume of the remaining solid .

5. Compute the mode for the following frequency distribution :

6. For what values of k , the given quadratic equation 9x² + 6kx + 4 = 0 has equal roots ?

OR

Three consecutive natural numbers are such that the square of the middle number exceeds the difference of the squares of the other two by 60. Find the numbers .

Section – B

[ 3 Marks Each ]

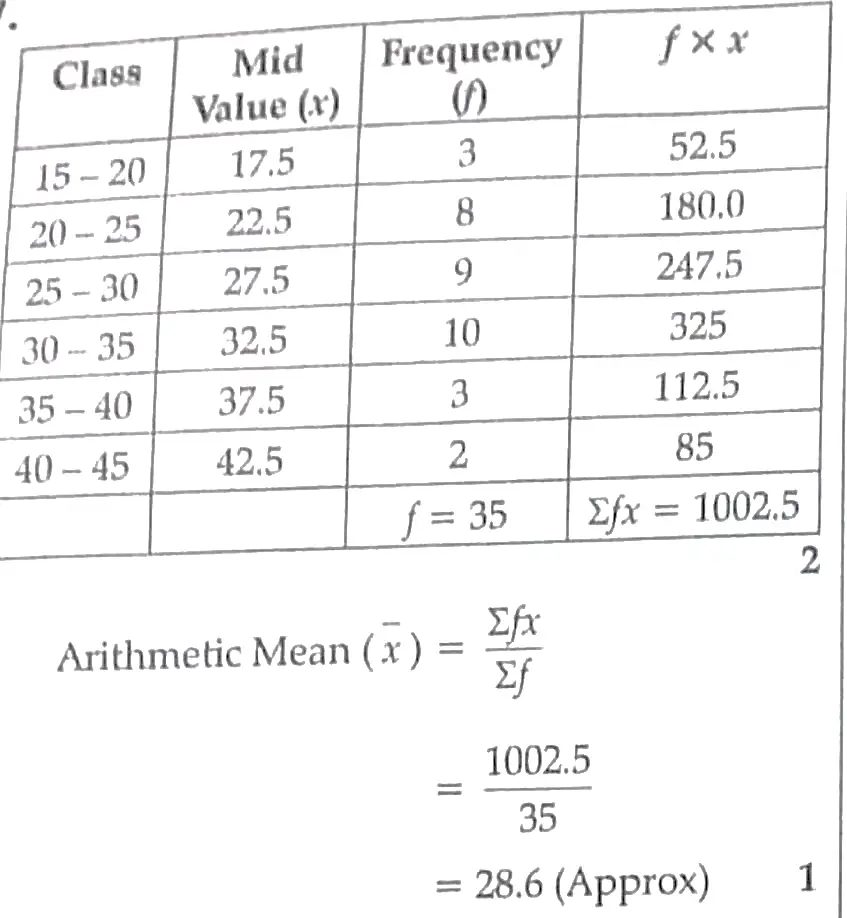
7. Find the arithmetic mean of the following frequency distribution :

8. Draw a line AB of length 9 cm . With A and B as centres , draw circles of radius 5 cm and 3 cm respectively . Construct tangents to each circle from the centre of the other circle .

9. The median of the following data is 525. Find the values of x and y , if total frequency is 100 .

10. The two palm trees are of equal heights and are standing opposite to each other on either side of the river , which is 80 m wide . From a point O between them on the river the angles of elevation of the top of the trees are 60 ° and 30 ° , respectively . Find the height of the trees and the distances of the point O from the trees . ( use √3 = 1.73 )

OR

The ratio of the length of a vertical rod and the length of its shadow is 1 : √3 . Find the angle of elevation of the Sun at that moment ?

Section – C

[ 4 Marks Each ]

11. A solid is in the shape of a cone mounted on a hemisphere of same base radius . If the curved surface areas of the hemispherical part and the conical part are equal , then find the ratio of the radius and the height of the conical part .

12. PQ is a tangent to a circle with centre O at point P. If △OPQ is an isosceles triangle , then find ∠OOP .

OR

The radii of two concentric circles are 13 cm and 8 cm . AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and intersecting the larger circle at P on producing . Find the length of AP .

Case Study – 1

13. ‘ Skysails ‘ is that genre of engineering science that uses extensive utilization of wind energy to move a vessel in the sea water . The sky sails technology allows the towing kite to gain a height of anything between 100 m to 300 m . The sailing kite is made in such a way that it can be raised to its proper elevation and then brought back with the help of a telescopic mast that enables the kite to be raised properly and effectively .

Based on the following figure related to sky sailing answer the questions :

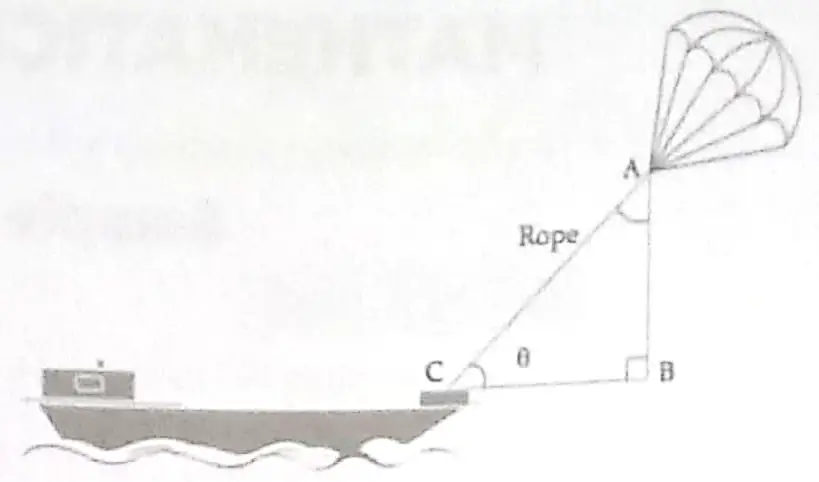
( i ) In the given figure , if tan θ = cot ( 30 ° + θ ) , where Q and 30 ° + θ are acute angles , then the value of θ .               [ 2 ]

( ii ) Find the value of tan 30 ° . cot 60 ° .           [ 2 ]

Case Study – 2

14. A ladder has rungs 25 cm apart . ( see the below ) .

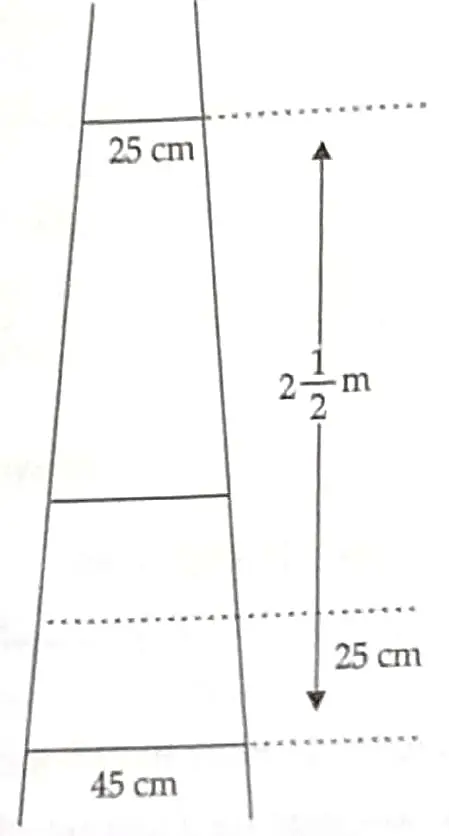
The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top . The top and the bottom rungs are 2 ½ m apart . ( i ) Find the number of the rungs :        [ 2 ]

( ii ) What is the length of the wood required for the rungs ?              [ 2 ]

Solution of Sample Paper

Section – A

1. Since , n^th term ( a_n ) = a + ( n – 1 ) d

Let a_n be zero a_n = 0

0 = 27 + ( n – 1 ) ( – 3 )            1

30 = 3n

n = 10                   1

10^th term of the given A.P. is zero .

Detailed Solution :

Given A.P. = 27 , 24 , 21 ,………. .

Here , a = 27 and d = 24 – 27 = -3

and , a_n = 0

∴ a_n = a + ( n − 1 ) d              1

⇒ 0 = 27 + ( n – 1 ) ( – 3 )

⇒ -3n + 3 = -27

⇒ -3n = -27 – 3 = -30

⇒ n = 10 .             1

OR

Since , a_n = a + ( n – 1 ) d

4 = a + 6 × ( -4 )             1

a = 28             1

Detailed Solution :

We have , d = -4 , n = 7 and a_n = 4

∴ a_n = a + ( n − 1 ) d           1

⇒ 4 = a + ( 7 – 1 ) ( – 4 )

⇒ 4 = a + 6 ( -4 )

⇒ = a – 24

⇒ a = 4 + 24

⇒ a = 28 .                1

2. Given , x² + 7x + 10 = 0

Comparing with ax² + bx + c = 0 , we get

a = 1 , b = 7 and c = 10

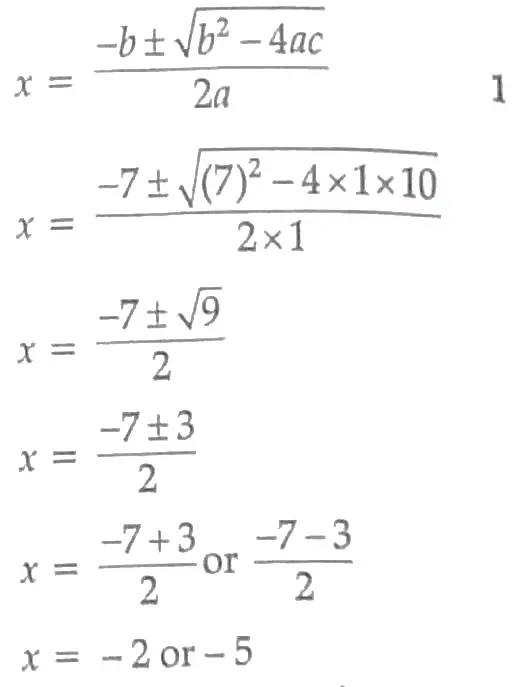
Hence , the roots of the given equation are – 2 and – 5 .              1

3. ∴ PQ = PT

PL + LQ = PM + MT

PL + LN = PM + MN ( LQ = LN , MT = MN ) ( Tangents to a circle from a common point )

Perimeter ( △PLM ) = PL + LM + PM         1

= PL + LN + MN + PM

= 2 ( PL + LN )

= 2 ( PL + LQ )

= 2 x 28 = 56 cm         1

Detailed Solution :

Given , PQ = 28 cm

∴ PQ = PT ( Length of tangents from an external point are equal )

i.e. , PQ = PT = 28 cm

According to figure ,

Let LQ = x , then

PL = ( 28 – x ) cm

and let MT = y , then

PM = ( 28 – y ) cm

and LM = LN + NM

= x + y

              1

Now , the perimeter of △PLM = PL + LM + PM

= ( 28 – x ) + ( x + y ) + ( 28 – y )

= 28 + 28 = 56 cm           1

4. Given , Height ( h ) = 14 cm

Base radius ( r ) = 6 cm

Volume of the remaining solid = Volume of a right circular cylinder – Volume of a right circular cone          ½

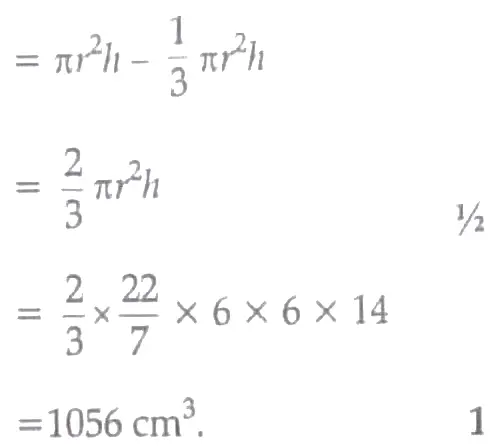
5. Here , modal class = 12 – 16

∴ l₁ = 12 , f₁ = 17 , f₀ = 9, f₂ = 12 and h = 4 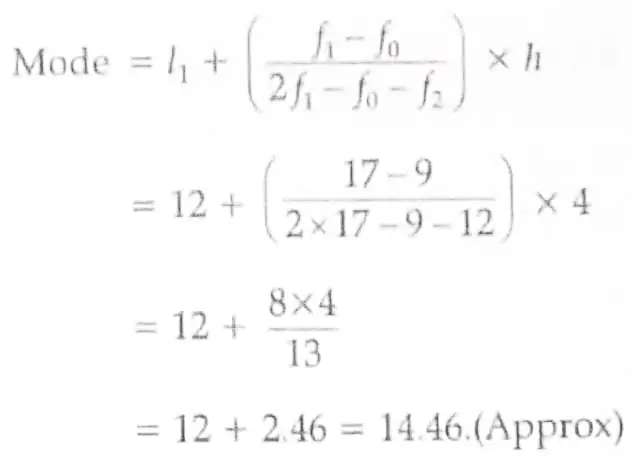           1

              1

6 . 9x² + 6kx + 4 = 0

For equal roots , b² – 4ac = 0

Discriminant , D = 0

So , ( 6k ) ² – 4 x 9 x 4 = 0             1

36k² = 144

k² = 4

k = ± 2             1

Detailed Solution :

Given , 9x² + 6kx + 4 = 0 .

Comparing with ax² + bx + c = 0 ,

we get a = 9 , b = 6k , c = 4             1

Since , Discriminant , D = b² – 4ac

For equal roots , D = 0

b² – 4ac = 0

⇒ ( 6k )² – 4 x 9 x 4 = 0

⇒ 36k² – 144 = 0

⇒ 36k² = 144

⇒ k² = 4

⇒ k = ± 2            1

OR

Let the three consecutive natural numbers be x , x + 1 and x + 2 .              ½

∴ ( x + 1 ) ² = ( x + 2 ) ²- ( x ) ² + 60

⇒ x² + 2x + 1 = x² + 4x + 4 – x² + 60

⇒ x² – 2x – 63 = 0           ½

⇒ x² – 9x + 7x – 63 = 0

⇒ x ( x – 9 ) + 7 ( x – 9 ) = 0

⇒ ( x – 9 ) ( x + 7 ) = 0

Thus , x = 9 or x = -7

Rejecting -7 , we get x = 9

Hence , three numbers are 9 , 10 and 11 .               1

Section – B

7 .

8.

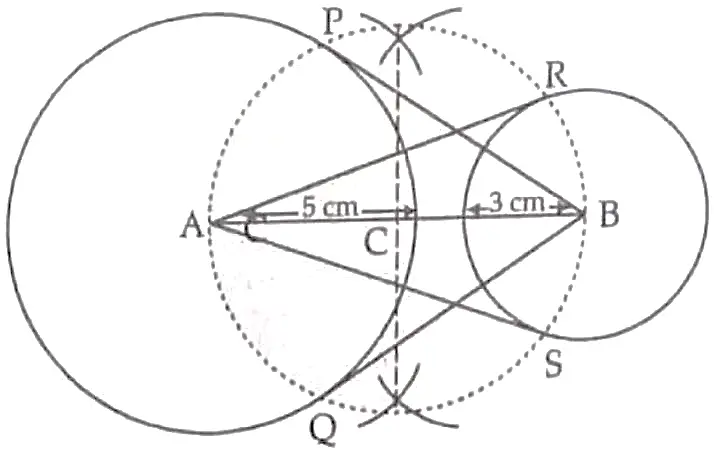            3

Detailed Solution :

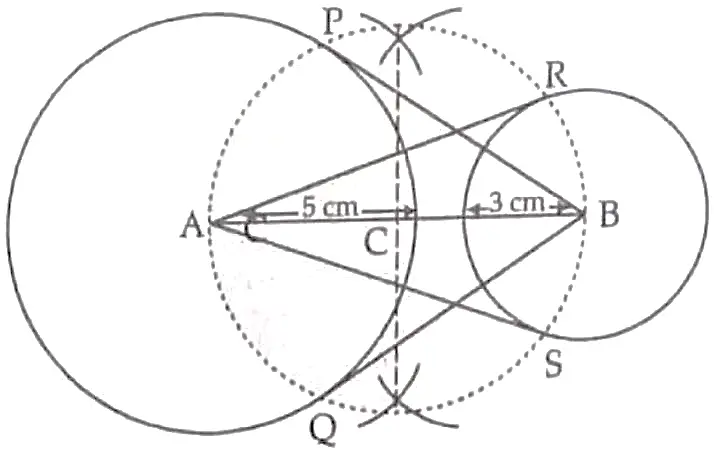               2

Steps of Construction :

( i ) Draw a line segment AB of 9 cm .

( ii ) Taking A and B as centres draw two circles of radii 5 cm and 3 cm respectively .

( iii ) Perpendicular bisect the line AB . Let mid point of AB be C.

( iv ) Taking C as centre draw a circle of radius AC which intersects the two circles at point P , Q , R and S.

( v ) Join BP , BQ , AS and AR .          1

BP , BQ and AR , AS are the required tangents .

9 .

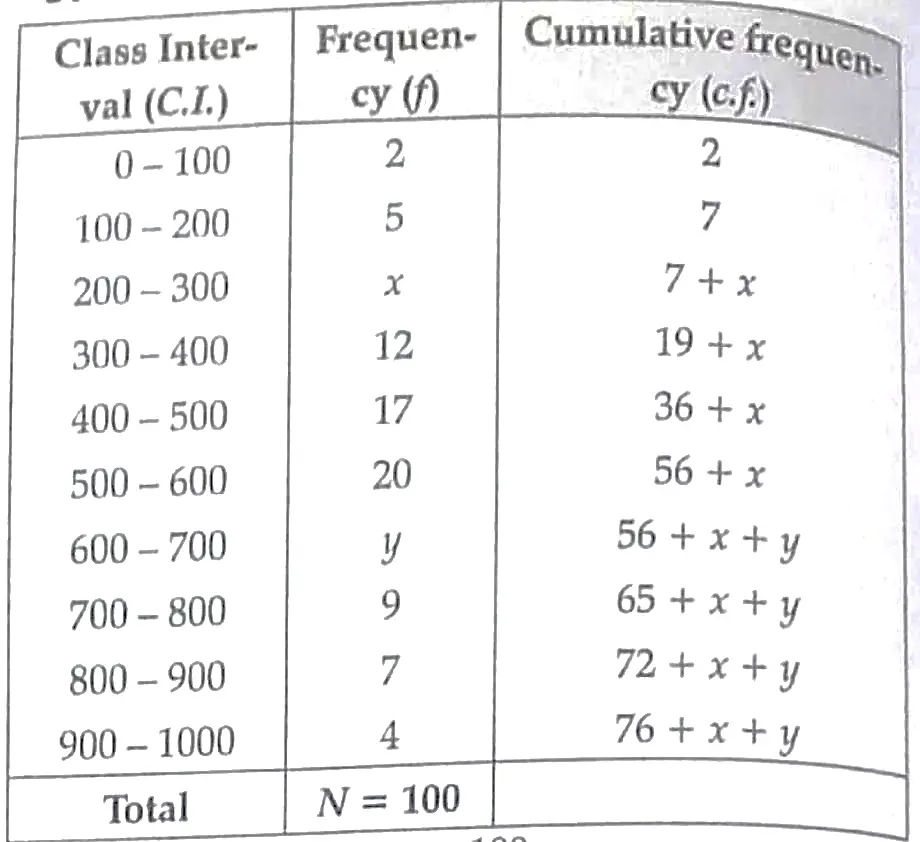               1

Also , 76 + x + y = 100

⇒ x + y = 100 – 76 = 24             …..( i )

Given , Median = 525 , which lies between class 500-600 .

⇒ Median class = 500 – 600

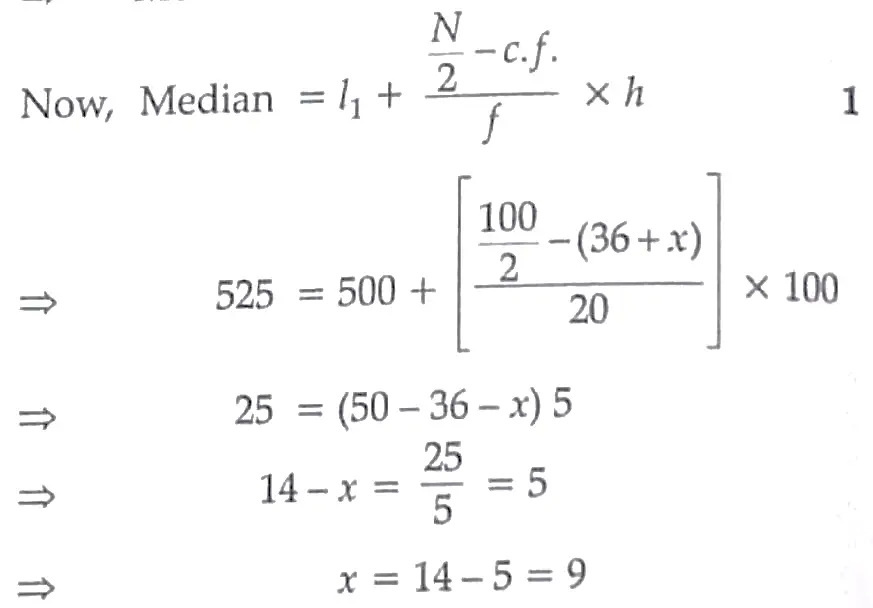
Putting the value of x in eq . ( i ) , we get

y = 24 – 9 = 15                1

Hence , x = 9 and y = 15 .

10.

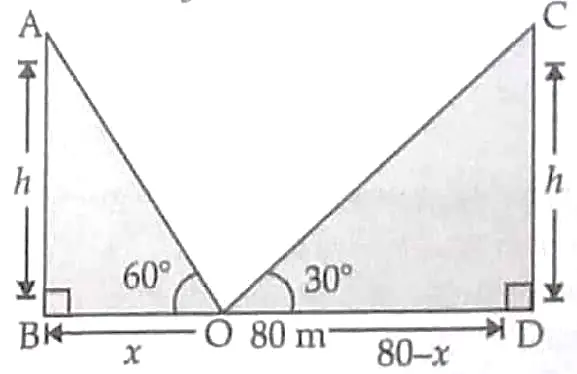
Let BD = width of river = 80 m

AB = CD = height of both trees = h

BO = x

OD = 80 – x

In △ABO , ∠B = 90 °

tan 60⁰ = h/x                 ½

√3 = h/x                ½

h = √3x           ……( i )

In △CDO , ∠D = 90 °

tan 30 ° = h / ( 80 – x )                ½

1 / √3 = h / ( 80 – x )             ……( ii )       ½

Solving ( i ) and ( ii ) , we get

x = 20 m

h = √3x      [ From eqn . ( i ) ]

= 1.73 x 20 m

= 34.6 m

The height of the trees = h = 34.6 m            ½

BO = x = 20 m

DO = 80 – x

= 80 – 20

= 60 m              ½

The distances of the point O from the trees are 20 m and 60 m respectively .

OR

Let AB be a vertical rod and BC be its shadow .

From the figure , ∠ACB = θ .

In △ABC , ∠B = 90 °

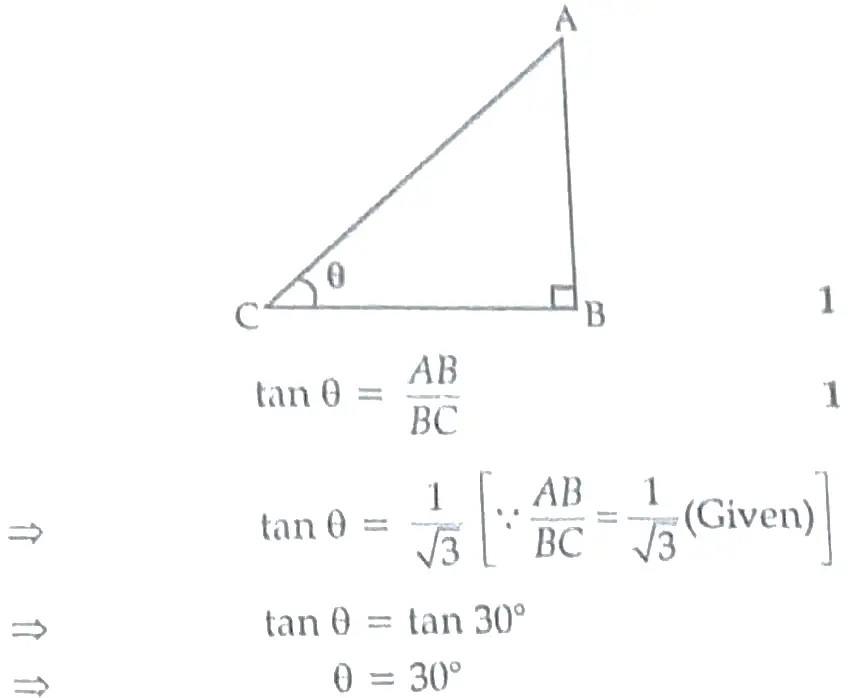
Hence , the angle of elevation of the Sun is 30 ° .            1

Section – C

11. Let ABC be a cone , which is mounted on a hemisphere .

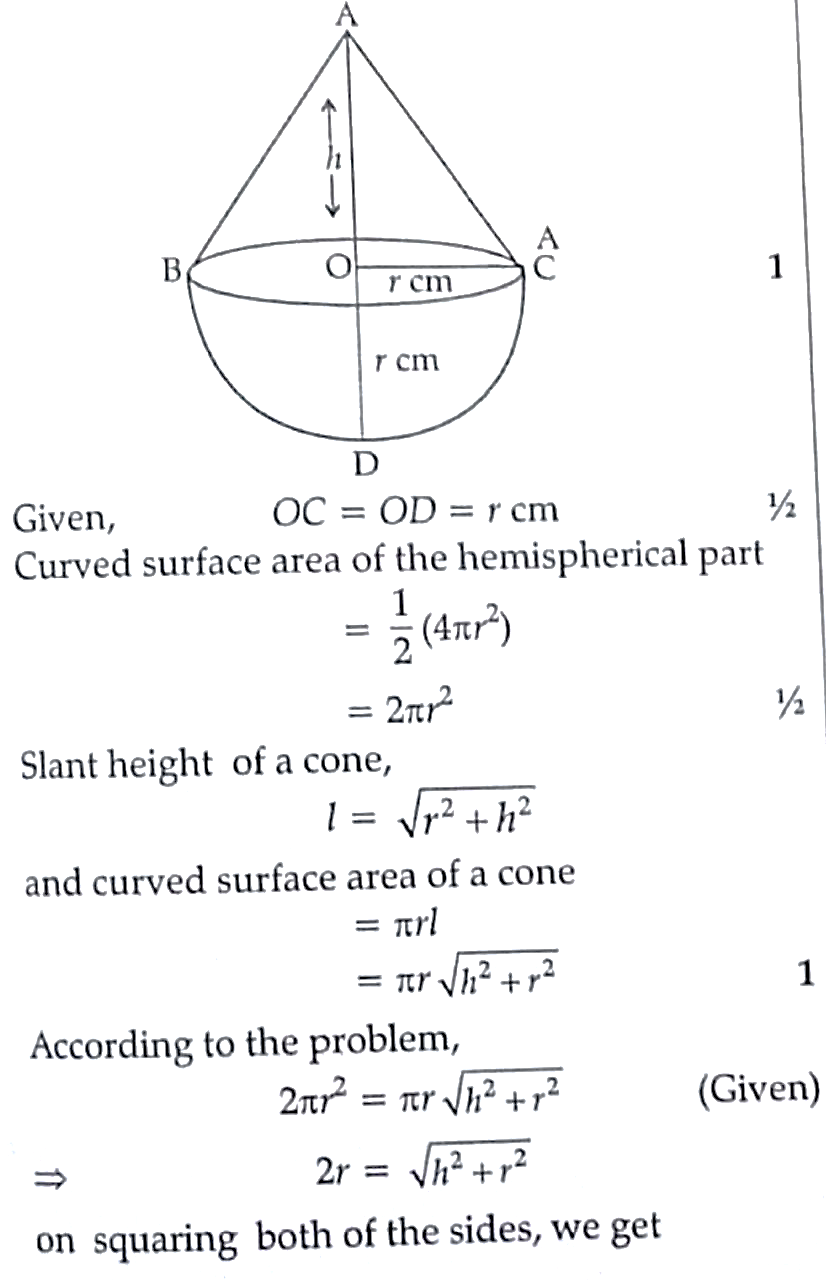
4r² = h² + r²

⇒ 4r² – r² = h²

⇒ 3r² = h²

⇒ r² / h² = 1 / 3

⇒ r / h = 1 / √3

Hence , the ratio of the radius and the height of conical part

= 1 : √3 .             1

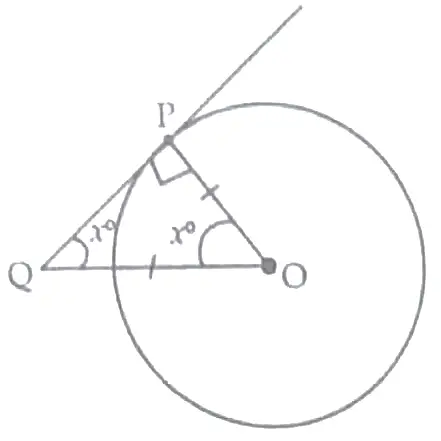
12 .

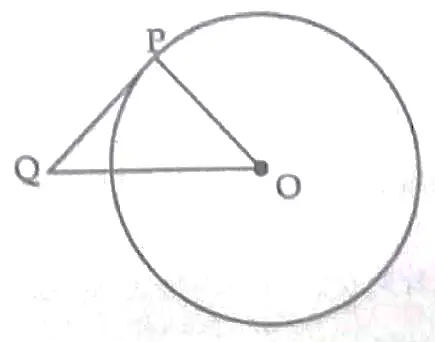
In △OPQ ,

∠P + ∠Q + ∠O = 180 ° ( ∠O = ∠Q , isosceles triangle )

2∠Q + ∠P = 180 °

2∠Q + 90 ° = 180 °

2∠Q = 90 °

∠Q = 45 °               4

Detailed Solution :

Since , ∠OPQ = 90 ° ( Angle between tangent and radius )

Let ∠PQO be x° , then

∠QOP = x°      ( Since OPQ is an isosceles triangle ) ( OP = OQ ) ( given )                   1

            1

In △OPQ ,

∠OPQ + ∠PQO + ∠QOP = 180 ° ( Sum of the angles of a triangle )

∴ 90 ° + x + x = 180 °          1

⇒ 2x = 180 ° – 90 ° = 90 °

⇒ x = 90 ° / 2 = 45 °

Hence , ∠OQP is 45 °        1

OR

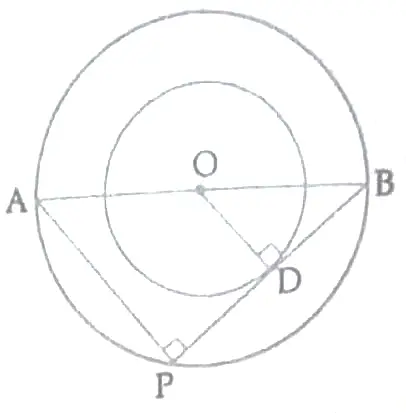             1

∠APB = 90 ° ( angle in semi – circle )

and ∠ODB = 90 ° ( radius is perpendicular to tangent )

⇒ △ABP ~ △OBD

⇒ AB / OB = AP / OD          1

⇒ 26 / 13 = AP / 8

Hence , AP = 16 cm           2

Case Study – 1

13. ( i ) Given , tan θ = cot ( 30 ° + θ )

= tan [ 90 ° – ( 30 ° + θ ) ]

= tan ( 90 ° – 30 ° – θ )

⇒ tan θ = tan ( 60 ° – θ )          1

⇒ θ = 60 ° – θ

⇒ 2θ = 60 °

⇒ θ = 30 °            1

( ii ) tan 30 ° = 1 / √3          ½

cot 60 ° = 1 / √3              ½

Now , tan 30 ° x cot 60 ° = 1 / √3 x 1 / √3

= 1 / 3          1

Case Study – 2

14. ( i ) The distance between the two rungs is 25 cm .            1

Hence , the total number of rungs

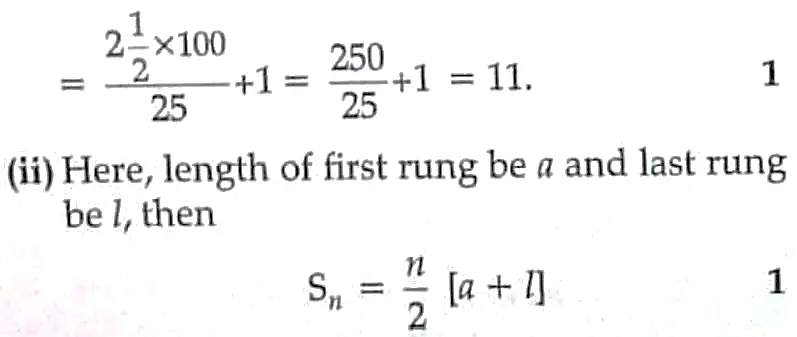
Here , a = 25, l = 45

and n = 11

Then ,

the required length of the wood ,

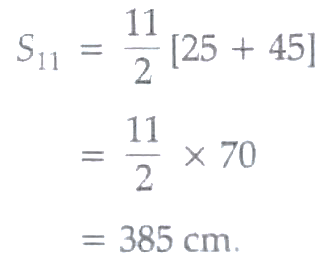           1