NCERT Notes For Class 11 Physics Chapter 2 Units And Measurements

CHAPTER 2: UNITS AND MEASUREMENT

Physical quantity

• Any quantity that can be measured
• A physical quantity can be classified into two:-

1. Fundamental quantity (Base quantity)
2. Derived quantity

• Quantities that cannot be expressed in terms of other quantities are known as fundamental quantities.

Eg:- mass, length, time, etc.

• Quantities which are derived from fundamental quantities are known as derived quantities. Eg:- force, velocity, area, volume, etc.

Unit

• A basic, internationally accepted reference standard used for measurement is called unit.
• The units for the fundamental or base quantities are called fundamental or base units.
• The units of all other physical quantities can be expressed as combinations of the base units.
• Units obtained for the derived quantities are called derived units.

Systems of Units

• A complete set of the base units and derived units is known as the system of units.
• In CGS system the base units for length, mass, and time were centimetres, grams, and second respectively.
• In FPS system the base units for length, mass and time were foot, pound and secondrespectively.
• In MKS system the base units for length, mass and time were metre, kilogram and second respectively.

THE INTERNATIONAL SYSTEM OF UNITS

• SI system is the internationally accepted system of unit at present.
• In SI, there are seven base units and two supplementary units.

Sl No	Base quantity	SI Units
		Name	Symbol
1	Length	metre	m
2	Mass	kilogram	kg
3	Time	second	s
4	Electric Current	ampere	A
5	Temperature	kelvin	K
6	Amount of substance	mole	mol
7	Luminous intensity	candela	cd
Sl No	Supplementary quantity	SI Units

		Name	symbol
1	Plane angle	radian	rad
2	Solid angle	steradian	sr

Plane angle

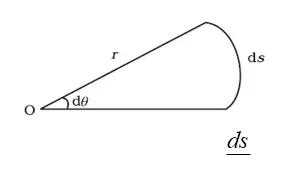
The plane angle , dθ = ds/r

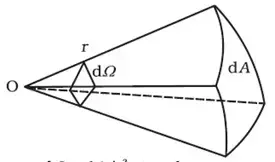
Solid angle

Thus percentage error in R

δR = 5% + 2% = 7%

Error in case of a measured quantity raised to a power

The relative error in a physical quantity raised to the power k is the k times the relative error in the individual quantity.

Thus, for Z = A^k , the relative error is given by

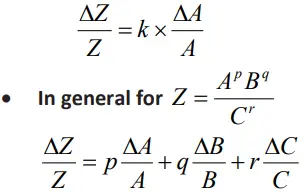
PROBLEM-1

Solution

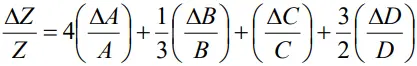
SIGNIFICANT FIGURES

• The number of digits in a measurement about which we are certain and one additional digit which is uncertain is known as significant figures.
• The number of significant figures indicates the accuracy with which the quantity is measured.

RULES FOR DETERMINING SIGNIFICANT FIGURES

• All the non-zero digits are significant and the zeros between the nonzero digits are significant.
• If the number is less than 1, the zero(s) on the right of the decimal point but to the left of the first non-zero digit are not significant.

Eg: In 0.00 2308, the underlined zeroes are not significant.

• The terminal or trailing zero(s) in a number without a decimal point are not significant.

Eg: Thus 123 m = 12300 cm = 123000 mm has three significant figures, the trailing zero(s) being not significant

• The trailing zero(s) in a number with a decimal point are significant.

Eg: The numbers 3.500 or 0.06900 have four significant figures each.

PROBLEM-1

• State the number of significant figures in the following:

a)0.007m² b) 2.64 x 10²⁴ kg c) 0.2370 g cm^-3

d) 6.320 J e) 6.032 Nm^-2 f) 0.0006032 m².

Solution

a)1   b) 3   c) 4   d) 4   e) 4   f) 4

Scientific Notation

• In this notation, every number is expressed as a x 10^b.
• where a is a number between 1 and 10, and b is any positive or negative exponent (or power) of 10.

Order of magnitude of a physical quantity

• in scientific notation, to get an approximate idea of the number, we may round off the number a to 1 (for a ≤ 5) and to 10 (for 5<a ≤ 10).
• Then the number can be expressed approximately as 10b in which the exponent (or power) b of 10 is called order of magnitude of the physical quantity.
• For example, the diameter of the earth (1.28×10⁷m) is of the order of 10⁷m with the order of magnitude 7.

Rules for arithmetic operation with significant figures Multiplication / Division

• In multiplication or division, the final result should retain as many significant figures as are there in the original number with the least significant figures.

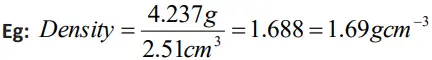
Addition or subtraction

• In addition or subtraction, the final result should retain as many decimal places as are there in the number with the least decimal places.
• For example,

436.32 g + 227.2 g + 0.301 g = 663.821 g = 663.8 g.

Rounding off the uncertain digit

• If the insignificant digit to be dropped is more than 5 preceding digit is raised by 1
• Eg : 1.68 =1.7 to 2 significant figures
• If the insignificant digit to be dropped is less than 5. it is left unchanged.
• Eg: 1.62=1.6 to 2 significant figures .

If the insignificant digit is 5:

• if the preceding digit is even, the insignificant digit is simply dropped and if it is odd, the preceding digit is raised by 1.

Eg: 2.745 =2.74 and 2.735 =2.74

PROBLEM-1

• Each side of a cube is measured to be 7.203 m. What are the total surface area and the volume of the cube to appropriate significant figures?

Solution

• The number of significant figures in the measured length is 4. The calculated area and the volume should therefore be rounded off to 4 significant figures.
• Surface area,

= 6 x (7.203)² = 311.299254m² = 311.3m²

• Volume

=(7.203)³ = 373.714754m³ = 373.7m³

PROBLEM -2

If the length and breadth of a thin rectangular sheet are measured, using a meter scale as 16.2 cm and 10.1 cm respectively. Express length and breadth in proper error limits. Also calculate area of the rectangular sheet with error limits.

Solution

• The least count of the meter scale = 0.1 cm, this will be equal to the absolute error (Δl).
• Thus, length can be expressed as

l =16.2 ± 0.1cm

• The percentage error in length can be calculated as

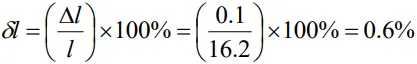
• There fore length can also be written as

l =16.2cm ± 0.6%

• Similarly, breadth can be written as

63.62 1.6% 2 A or b =10.1cm ±1%

• Area is given by

A = lb = 163.62cm² ± 1.6% or A = 163.62 ± 2.6cm²

• In proper significant figures ,area

A = 164 ± 3cm²

DIMENSIONS OF PHYSICAL QUANTITIES

• All the physical quantities represented by derived units can be expressed in terms of some combination of seven fundamental or base quantities.
• The dimensions of a physical quantity are the powers (or exponents) to which the base quantities are raised to represent that quantity.
• Length has the dimension [L], mass [M], time [T], electric current [A], thermodynamic temperature [K], luminous intensity [cd], and amount of substance [mol].
• In mechanics, all the physical quantities can be written in terms of the dimensions [L], [M] and [T].

Dimensional formulae

• The expression which shows how and which of the base quantities represent the dimensions of physical quantity is called the dimensional formula of the given physical quantity.
• For example, the dimensional formula of the volume is [M⁰L³T⁰].

Dimensional equation

• An equation obtained by equating a physical quantity with its dimensional formula is called the dimensional equation of the physical quantity.
• For example, the dimensional equations of volume [V], speed [v], force [F ] and mass density [] may be expressed as

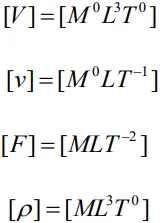
APPLICATIONS OF DIMENSIONAL ANALYSIS

• Dimensional analysis can be used to:

a)To check the dimensional consistency of equations

b)To deduce relation among physical quantities.

To check the dimensional consistency of equations

• The principle of homogeneity is used to check the dimensional correctness of equations.

Principle of homogeneity

• The magnitudes of physical quantities may be added together or subtracted from one another only if they have the same dimensions.
• The equation P = AB + CD , is dimensionally correct only if [P] = [AB] = [CD].

PROBLEM-1

• Check the dimensional consistency of the equation v = u + at .

Solution

We have , [v] = [M⁰LT^-1]

[u] = [M⁰LT^-1]

[at] = [M⁰LT^-2] [ T] =[M⁰LT^-1]

Thus [v] =[u] =[at] , the equation is dimensionally correct.

Limitations of dimensional analysis

• The dimensional consistency does not guarantee correct equations.
• The arguments of special functions, such as the trigonometric, logarithmic and exponential functions are dimensionless.
• A pure number, ratio of similar physical quantities, such as angle as the ratio (length/length), refractive index as the ratio (speed of light in vacuum/speed of light in medium) etc., has no dimensions.
• Dimensionless constants cannot be obtained by this method.
• If an equation fails consistency test, it is proved wrong, but if it passes, it is not proved right.
• It does not distinguish between the physical quantities having same dimensions.

To deduce relation among physical quantities

• For this we should know dependence of the physical quantity on other quantities and consider it as a product type of the dependence.

Derivation of the equation for time period of a pendulum using dimensions

• Let the period of oscillation of the simple pendulum depends on its length (l), mass of the bob (m) and acceleration due to gravity (g).
• The dependence of time period T on the quantities l, g and m as a product may be written as : t = kl^xg ^ym^z
• Where k is a constant
• Taking dimensions on both sides

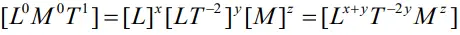
• On equating the dimensions on both sides, we get

x+y =0 , thus x= – y

z=0 , -2y =1, thus y = -1/2

therefore x= ½.

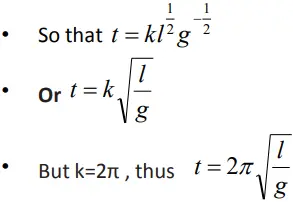
The solid angle , dΩ = dA/r²

Prefixes used with SI units

Prefix	Symbol	Meaning
Tera –	T	1012
Giga-	G	109
Mega-	M	106
Kilo-	K	103
Deci-	d	10-1
Centi –	c	10-2
Milli-	m	10-3
Micro	µ	10-6
Nano	n	10-9
Pico	p	10-12

MEASUREMENT OF LENGTH

• A metre scale is used for lengths from 10^-3 m to 10²m.
• A vernier callipers is used for lengths to an accuracy of 10^-4m.
• A screw gauge and a spherometer can be used to measure lengths as less as to 10^-5m.

Measurement of large distances

Parallax method

• A method to measure distances to far away objects.
• The apparent shift in the position of an object when viewed from two different positions is known as parallax.
• The distance between the two points of observation is called the basis.

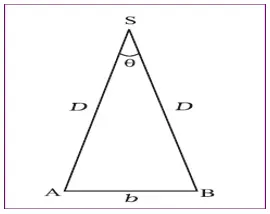
• The star is viewed from two different positions from earth and the angle is measured.
• By using the equation , Angle = Arc/Radius , we get

θ = b /D

• Therefore D = b/θ

Parallax method to find diameter of a star

• Two diametrically opposite points on star are viewed from the same location on the earth and α is measured.
• If d is the diameter of the planet

α = d/ D

• Therefore d =α ×D , where D- distance to the star.

PROBLEM -1

• Calculate the angle of (a) 1⁰ (degree) , (b) 1′ (minute of arc or arcmin) and (c) 1″ (second of arc or arc second) in radians. Use 360⁰=2π rad, 1⁰=60′ and1′ = 60 ″

Solution

PROBLEM -2

• The moon is observed from two diametrically opposite points A and B on Earth. The angle θ subtended at the moon by the two directions of observation is 1^o 54′ . Given the diameter of the Earth to be about 1.276 × 10⁷ m, compute the distance of the moon from the Earth.

Solution

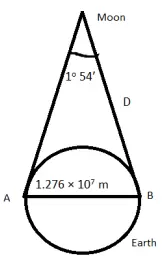
We have

θ =1^o 54′=114’=114×2.91×10^-4rad=3.32×10^-2rad

b=AB=1.276×10⁷ m

Therefore the earth-moon distance

D = b/θ = 1.276×10⁷/3.32×10^-2 = 3.84×10⁸m

PROBLEM -3

• The Sun’s angular diameter is measured to be 1920′′. The distance D of the Sun from the Earth is 1.496 × 10¹¹ m. What is the diameter of the Sun ?

Solution

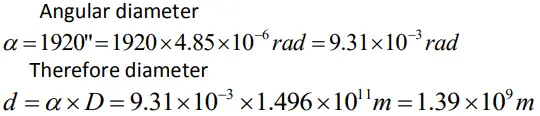
Estimation of Very Small Distances

• To measure the size of a molecule, special methods like thin film techniques are used.
• Electron microscopes can almost resolve atoms or molecule in a material.
• In recent times, tunnelling microscopy has been developed in which again the limit of resolution is better than an angstrom.

SPECIAL UNITS FOR SHORT AND LARGE LENGTHS

Sl No	Unit Name	Symbol	Meaning
1	fermi	f	10-15 m
2	angstrom	A0	10-10 m
3	Astronomical unit	AU	1.496 x1011 m (Average distance of the sun from earth )
4	light year	ly	9.46 x1015 m ( distance that light travels with velocity of 3 x 108 m/s in one year )
5	parsec	parsec	3.08 x 1016 m (distance at which average radius of earth’s orbit subtends an angle of 1 arc second)

MEASUREMENT OF MASS

• The unit used to measure mass of atoms or molecules is unified atomic mass unit (u). 1u = 1.66 x 10^-27kg
• Mass of commonly available objects can be determined by a common balance.
• Large masses in the universe like planets, stars, etc., can be measured by using gravitational method.
• For measurement of small masses of atomic/subatomic particles etc., we make use of mass spectrograph.

MEASUREMENT OF TIME

• To measure any time interval we need a clock.
• We now use an atomic standard of time, which is based on the periodic vibrations produced in a cesium atom- cesium clock or in general atomic clock.
• The cesium atomic clocks are very accurate.
• In our country, the NPL( National Physical Laboratory) has the responsibility of maintenance and improvement of physical standards, including that of time, frequency, etc.

ACCURACY AND PRECISION OF A MEASUREMENT

• Accuracy of a measurement is a measure of how close the measured value is to the true value of the quantity.
• Precision is the resolution or limit with which the quantity is measured.
• The accuracy may depend on the limit or resolution of the measuring instrument.

ERRORS IN MEASUREMENT

• Error is the uncertainty in a measurement.
• It is the difference between measured value and true value of the quantity.

TYPES OF ERRORS

• Errors can be classified as:

1. Systematic Errors
2. Random errors
3. Least count errors

Systematic errors

• The systematic errors are those errors that tend to be in one direction, either positive or negative.
• The sources of systematic errors are:

1. Instrumental errors -arise from the errors due to imperfect design or calibration of the measuring instrument, zero error in the instrument, etc.
2. Imperfection in experimental technique or procedure
3. Personal errors – arise due to an individual’s bias, lack of proper setting of the apparatus or individual’s carelessness in taking observations without observing proper precautions, parallax error, etc.

Minimizing systematic errors

• Systematic errors can be minimized by

1. Improving experimental techniques
2. Selecting better instruments
3. Removing personal bias as far as possible.

Random errors

• This error occurs irregularly and is random with respect to sign and size.
• Arise due to random and unpredictable fluctuations in experimental conditions, unbiased personal errors etc.
• Random errors can be minimized by repeating the observations several times.

Least count errors

• Least count is the smallest value that can be measured by an instrument.
• Least count error is the error associated with the resolution of the instrument.
• Least count errors can be minimized by :

1. Using instruments of higher precision
2. Improving experimental techniques

ESTIMATION OF ERRORS

• The arithmetic mean of all the observations in a measurement is taken as the true value of the quantity.in the absence of any other method knowing the true value.
• For n observations a₁, a₂,a₃,…..a_n , the true value of the quantity is given by

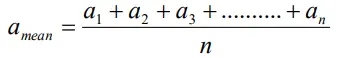
or

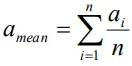
Absolute error ( |Δa| )

Absolute error is the magnitude of the difference between the true value of the quantity and the individual measurement value.

For n observations a1, a2,a3,…..an , the absolute errors in the measured values are given by

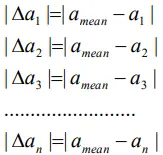
The absolute error will be always positive.

Mean absolute error( Δa_mean)

• The arithmetic mean of all the absolute errors is taken as the final or mean absolute error of the value of the physical quantity.
• Thus

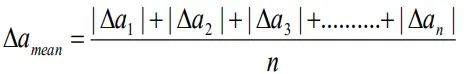
• or

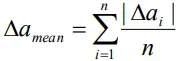
• Thus, any measured value can be written as

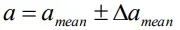
• That is any measurement ‘a’ of the physical quantity lies between a_mean ±Δa_mean and a_mean − Δa_mean

Relative error

• Ratio of the mean absolute error to the mean value of the quantity.

Percentage error (a)

• It is the relative error expressed in percentage.

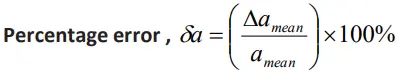
PROBLEM -1

We measure the period of oscillation of a simple pendulum. In successive measurements, the readings turn out to be 2.63 s, 2.56 s, 2.42 s, 2.71s and 2.80 s. Calculate the absolute errors, relative error or percentage error.

Solution

Given T₁=2.63s, T₂=2.56s, T₃ =2.42 s, T₄=2.71 s, T₅=2.80 s, T5=2.80 s

Mean period of oscillation

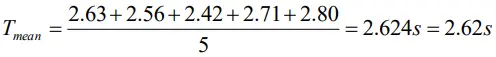
Absolute errors in the time period

Mean absolute error of time period

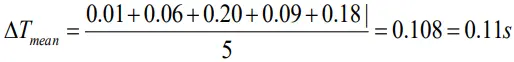
Thus, the period of oscillation of the pendulum lies between 2.62 + 0.11 and 2.62 – 0.11.or between 2.73 and 2.51.

Since the error is 0.11s , the value of time period can be written in a more correct way as

T = 2.6 ±0.1s

Relative error of time period

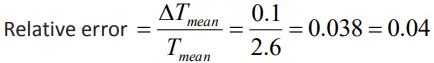
Percentage error

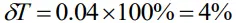
COMBINATION OF ERRORS

Error of a sum or a difference

• When two quantities are added or subtracted, the absolute error in the final result is the sum of the absolute errors in the individual quantities.
• Thus, for two quantities A and B, the absolute error in the sum or difference will be

ΔZ = ΔA+ ΔB

Where ΔZ – absolute error in sum or difference

ΔA – absolute error in A

ΔB – absolute error in B

Proof

PROBLEM

The temperatures of two bodies measured by a thermometer are t₁ = 20 ⁰C ± 0.5 ⁰C and t₂ = 50 ⁰C ± 0.5 ⁰C. Calculate the temperature difference and the error in it.

Solution

• The temperature difference

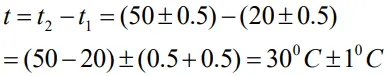
Error of a product or a quotient

• When two quantities are multiplied or divided, the relative error in the result is the sum of the relative errors in the multipliers.
• Thus, for two quantities A and B, the relative error in the product or quotient will be

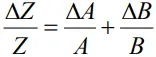
Proof

• For Z = AB, we may write

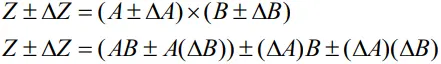
• Dividing LHS by Z and RHS by AB, we get

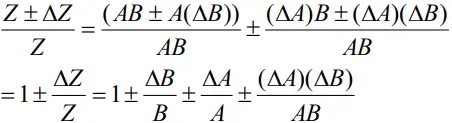
• Since ΔA and ΔB are small, we shall ignore their product.
• Thus, the maximum relative error is given by

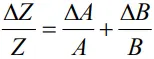
• This is true for the division also.
• For Z = A/B, we may write

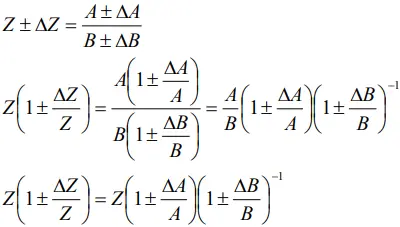
• By using the binomial theorem

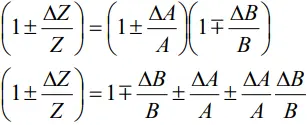
• Neglecting last term we get

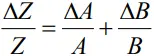
PROBLEM-1

• The resistance R = V/I where V = (100 ± 5)V and I = (10 ± 0.2)A. Find the percentage error in R.

Solution

Percentage error in V is given by

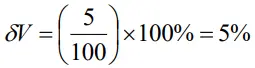
The percentage error in I is

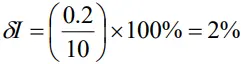
Thus percentage error in R

δR = 5% + 2% = 7%

Error in case of a measured quantity raised to a power

The relative error in a physical quantity raised to the power k is the k times the relative error in the individual quantity.

Thus, for Z = A^k , the relative error is given by

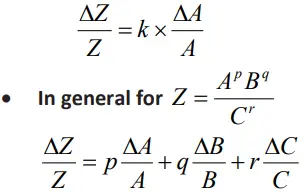
PROBLEM-1

Solution

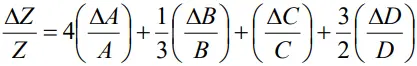
SIGNIFICANT FIGURES

• The number of digits in a measurement about which we are certain and one additional digit which is uncertain is known as significant figures.
• The number of significant figures indicates the accuracy with which the quantity is measured.

RULES FOR DETERMINING SIGNIFICANT FIGURES

• All the non-zero digits are significant and the zeros between the nonzero digits are significant.
• If the number is less than 1, the zero(s) on the right of the decimal point but to the left of the first non-zero digit are not significant.

Eg: In 0.00 2308, the underlined zeroes are not significant.

• The terminal or trailing zero(s) in a number without a decimal point are not significant.

Eg: Thus 123 m = 12300 cm = 123000 mm has three significant figures, the trailing zero(s) being not significant

• The trailing zero(s) in a number with a decimal point are significant.

Eg: The numbers 3.500 or 0.06900 have four significant figures each.

PROBLEM-1

• State the number of significant figures in the following:

a)0.007m² b) 2.64 x 10²⁴ kg c) 0.2370 g cm^-3

d) 6.320 J e) 6.032 Nm^-2 f) 0.0006032 m².

Solution

a)1   b) 3   c) 4   d) 4   e) 4   f) 4

Scientific Notation

• In this notation, every number is expressed as a x 10^b.
• where a is a number between 1 and 10, and b is any positive or negative exponent (or power) of 10.

Order of magnitude of a physical quantity

• in scientific notation, to get an approximate idea of the number, we may round off the number a to 1 (for a ≤ 5) and to 10 (for 5<a ≤ 10).
• Then the number can be expressed approximately as 10b in which the exponent (or power) b of 10 is called order of magnitude of the physical quantity.
• For example, the diameter of the earth (1.28×10⁷m) is of the order of 10⁷m with the order of magnitude 7.

Rules for arithmetic operation with significant figures Multiplication / Division

• In multiplication or division, the final result should retain as many significant figures as are there in the original number with the least significant figures.

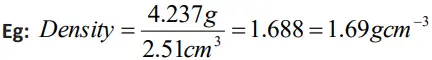
Addition or subtraction

• In addition or subtraction, the final result should retain as many decimal places as are there in the number with the least decimal places.
• For example,

436.32 g + 227.2 g + 0.301 g = 663.821 g = 663.8 g.

Rounding off the uncertain digit

• If the insignificant digit to be dropped is more than 5 preceding digit is raised by 1
• Eg : 1.68 =1.7 to 2 significant figures
• If the insignificant digit to be dropped is less than 5. it is left unchanged.
• Eg: 1.62=1.6 to 2 significant figures .

If the insignificant digit is 5:

• if the preceding digit is even, the insignificant digit is simply dropped and if it is odd, the preceding digit is raised by 1.

Eg: 2.745 =2.74 and 2.735 =2.74

PROBLEM-1

• Each side of a cube is measured to be 7.203 m. What are the total surface area and the volume of the cube to appropriate significant figures?

Solution

• The number of significant figures in the measured length is 4. The calculated area and the volume should therefore be rounded off to 4 significant figures.
• Surface area,

= 6 x (7.203)² = 311.299254m² = 311.3m²

• Volume

=(7.203)³ = 373.714754m³ = 373.7m³

PROBLEM -2

If the length and breadth of a thin rectangular sheet are measured, using a meter scale as 16.2 cm and 10.1 cm respectively. Express length and breadth in proper error limits. Also calculate area of the rectangular sheet with error limits.

Solution

• The least count of the meter scale = 0.1 cm, this will be equal to the absolute error (Δl).
• Thus, length can be expressed as

l =16.2 ± 0.1cm

• The percentage error in length can be calculated as

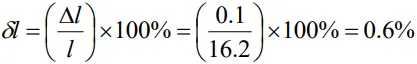
• Their fore length can also be written as

l =16.2cm ± 0.6%

• Similarly, breadth can be written as

63.62 1.6% 2 A or b =10.1cm ±1%

• Area is given by

A = lb = 163.62cm² ± 1.6% or A = 163.62 ± 2.6cm²

• In proper significant figures ,area

A = 164 ± 3cm²

DIMENSIONS OF PHYSICAL QUANTITIES

• All the physical quantities represented by derived units can be expressed in terms of some combination of seven fundamental or base quantities.
• The dimensions of a physical quantity are the powers (or exponents) to which the base quantities are raised to represent that quantity.
• Length has the dimension [L], mass [M], time [T], electric current [A], thermodynamic temperature [K], luminous intensity [cd], and amount of substance [mol].
• In mechanics, all the physical quantities can be written in terms of the dimensions [L], [M] and [T].

Dimensional formulae

• The expression which shows how and which of the base quantities represent the dimensions of physical quantity is called the dimensional formula of the given physical quantity.
• For example, the dimensional formula of the volume is [M⁰L³T⁰].

Dimensional equation

• An equation obtained by equating a physical quantity with its dimensional formula is called the dimensional equation of the physical quantity.
• For example, the dimensional equations of volume [V], speed [v], force [F ] and mass density [] may be expressed as

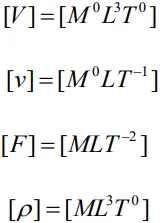
APPLICATIONS OF DIMENSIONAL ANALYSIS

• Dimensional analysis can be used to:

a)To check the dimensional consistency of equations

b)To deduce relation among physical quantities.

To check the dimensional consistency of equations

• The principle of homogeneity is used to check the dimensional correctness of equations.

Principle of homogeneity

• The magnitudes of physical quantities may be added together or subtracted from one another only if they have the same dimensions.
• The equation P = AB + CD , is dimensionally correct only if [P] = [AB] = [CD].

PROBLEM-1

• Check the dimensional consistency of the equation v = u + at .

Solution

We have , [v] = [M⁰LT^-1]

[u] = [M⁰LT^-1]

[at] = [M⁰LT^-2] [ T] =[M⁰LT^-1]

Thus [v] =[u] =[at] , the equation is dimensionally correct.

Limitations of dimensional analysis

• The dimensional consistency does not guarantee correct equations.
• The arguments of special functions, such as the trigonometric, logarithmic and exponential functions are dimensionless.
• A pure number, ratio of similar physical quantities, such as angle as the ratio (length/length), refractive index as the ratio (speed of light in vacuum/speed of light in medium) etc., has no dimensions.
• Dimensionless constants cannot be obtained by this method.
• If an equation fails consistency test, it is proved wrong, but if it passes, it is not proved right.
• It does not distinguish between the physical quantities having same dimensions.

To deduce relation among physical quantities

• For this we should know dependence of the physical quantity on other quantities and consider it as a product type of the dependence.

Derivation of the equation for time period of a pendulum using dimensions

• Let the period of oscillation of the simple pendulum depends on its length (l), mass of the bob (m) and acceleration due to gravity (g).
• The dependence of time period T on the quantities l, g and m as a product may be written as : t = kl^xg ^ym^z
• Where k is a constant
• Taking dimensions on both sides

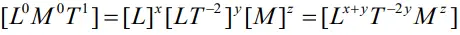
• On equating the dimensions on both sides, we get

x+y =0 , thus x= – y

z=0 , -2y =1, thus y = -1/2

therefore x= ½.

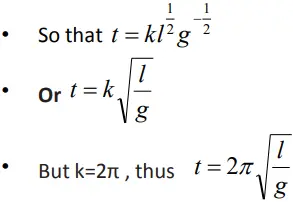
Also check: NCERT Notes For Class 11 Physics Chapter 3 Motion In A Straight Line