NCERT Notes For Class 11 Physics Chapter 3 Motion In A Straight Line

Class 11 Physics Chapter 3 Motion In A Straight Line

NCERT Notes For Class 11 Physics Chapter 3 Motion In A Straight Line, (Physics) exam are Students are taught thru NCERT books in some of state board and CBSE Schools.  As the chapter involves an end, there is an exercise provided to assist students prepare for evaluation.  Students need to clear up those exercises very well because the questions withinside the very last asked from those. 

Sometimes, students get stuck withinside the exercises and are not able to clear up all of the questions.  To assist students solve all of the questions and maintain their studies with out a doubt, we have provided step by step NCERT Notes for the students for all classes.  These answers will similarly help students in scoring better marks with the assist of properly illustrated Notes as a way to similarly assist the students and answering the questions right.

NCERT Notes For Class 11 Physics Chapter 3 Motion In A Straight Line

Class 11 Physics Chapter 3 Motion In A Straight Line

CHAPTER THREE: MOTION IN A STRAIGHT LINE

MOTION

• Motion is change in position of an object with time.
• Branch of physics which deals with the motion of objects – Mechanics
• Mechanics is classified into
• i)Statics ii) Kinematics iii) Dynamics
• Statics deals with object at rest under the action of forces.
• In Kinematics, we study ways to describe motion without going into the causes of motion.
• Dynamics deals with objects in motion by considering the causes of motion.

POINT OBJECT

• If the size of the object is much smaller than the distance it moves, it is considered as point object.

Examples

1. a railway carriage moving without jerks between two stations.
2. a monkey sitting on top of a man cycling smoothly on a circular track.

FRAME OF REFERENCE

• A place from which motion is observed and measured is called frame of reference.
• Example: Cartesian coordinate system with a clock – the reference point at the origin.

TYPES OF MOTION

• Based on the number of coordinates required to describe motion, motion can be classified as:

1. One dimensional motion (Rectilinear motion )
2. Two-dimensional motion
3. Three-dimensional motion.

One dimensional motion

• Motion along a straight line is called one dimensional motion or rectilinear motion.
• Only one coordinate is required to describe this motion.
• In one-dimensional motion, there are only two directions (backward and forward, upward and downward) in which an object can move

Example:

1. a car moving on a straight road.
2. Freely falling body

Two-dimensional motion

• Motion in a plane is called two dimensional motions.
• Two coordinates are required to represent this motion.

Example :

1. A car moving on a plane ground
2. A boat moving on a still lake

Three-dimensional motion

Motion in a space is called three dimensional motion.

Three coordinates are required to represent this motion.

Example:

1. Movement of gas molecules
2. A flying bird

PATH LENGTH

• The length of the path covered by an object is called path length.
• It is the total distance travelled by the object.
• Path length is a scalar quantity — a quantity that has a magnitude only and no direction.

• For example, the path length of the car moving from O to P and then from P to Q is 360+120 = 480 m.

DISPLACEMENT

• It is the change of position in a definite direction.
• Displacement is a vector quantity –have both magnitude and direction.
• It can be positive, negative or zero.
• In one dimensional motion direction, the two directions can be represented using positive (+) and negative (-) signs.
• If x₁ and x₂ are the positions of an object in time t₁ and t₂, the displacement in time interval

Δt = t₂ − t₁ , is given by

Δx = x₂ − x₁

• If x2 > x1 , displacement is positive
• if x2 < x1 , displacement is negative.
• The magnitude of displacement may or may not be equal to the path length traversed by an object.
• If the motion of an object is along a straight line and in the same direction, the magnitude of displacement is equal to the total path length.

Uniform motion

• If an object moving along the straight line covers equal distances in equal intervals of time, it is said to be in uniform motion along a straight line.

AVERAGE VELOCITY

• Ratio of total displacement to the total time.

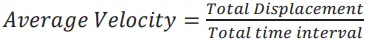
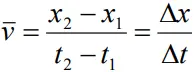
• The SI unit for velocity is m/s or m s^–1
• The unit km h^–1 is used in many everyday applications

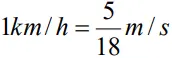
• Average velocity is a vector quantity
• Average velocity can be positive or negative or zero.
• Slope of the Displacement-Time graph gives the average velocity.

AVERAGE SPEED

• Ratio of total path length travelled to the total time interval

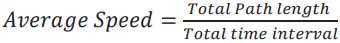
• Average speed over a finite interval of time is greater or equal to the magnitude of the average velocity
• If the motion of an object is along a straight line and in the same direction, the magnitude of average velocity is equal to average speed.
• SI unit of average speed is same as that of velocity.

PROBLEM

• A car is moving along a straight line, It moves from O to P in 18 s and returns from P to Q in 6.0 s. What are the average velocity and average speed of the car in going (a) from O to P ? and (b) from O to P and back to Q ?

Solution

1. Average velocity

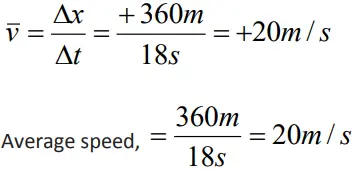
1. Average velocity

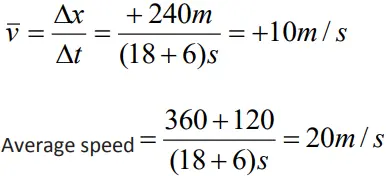
INSTANTANEOUS VELOCITY ( VELOCITY)

• It is the velocity of an object at an instant.
• It is the average velocity as the time interval tends to zero

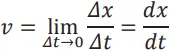
• For uniform motion, velocity is the same as the average velocity at all instants.

INSTANTANEOUS SPEED (SPEED)

• Instantaneous speed or simply speed is the magnitude of velocity
• Instantaneous speed at an instant is equal to the magnitude of the instantaneous velocity at that instant because for an infinitesimally small time interval, the motion of a particle can be approximated to be uniform.

AVERAGE ACCELERATION

• Ratio of change in velocity to time interval

       

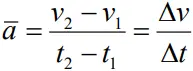
• Where v₂ and v₁ are the instantaneous velocities or simply velocities at time t₂ and t₁ .
• SI unit is m/s².
• Slope of the velocity-time graph gives average acceleration.

INSTANTANEOUS ACCELERATION (ACCELERATION)

• It is the acceleration at an instant.
• It is the average acceleration as the as the time interval tends to zero

         

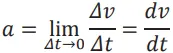
• The instantaneous acceleration is the slope of the tangent to the v–t curve at that instant.
• Acceleration can be positive, negative or zero.
• It is a vector quantity.

GRAPHS RELATED TO MOTION

POSITION-TIME GRAPH ( x –t Graph)

• It is the graph drawn taking time along x-axis and position along y-axis
• Slope of the x-t graph gives the average velocity.
• Slope of the tangent at a point in the x-t graph gives the velocity at that point.

Uses of Position –Time Graph

• To find the position at any instant
• To find the velocity at any instant
• To obtain the nature of motion

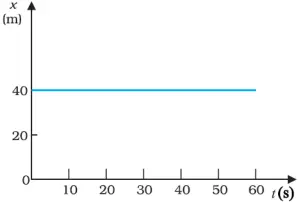
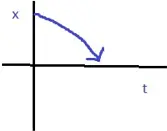
Position- time graph of stationary object

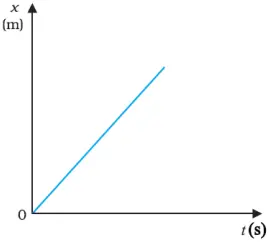
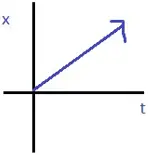
Position- time graph of an object in uniform motion

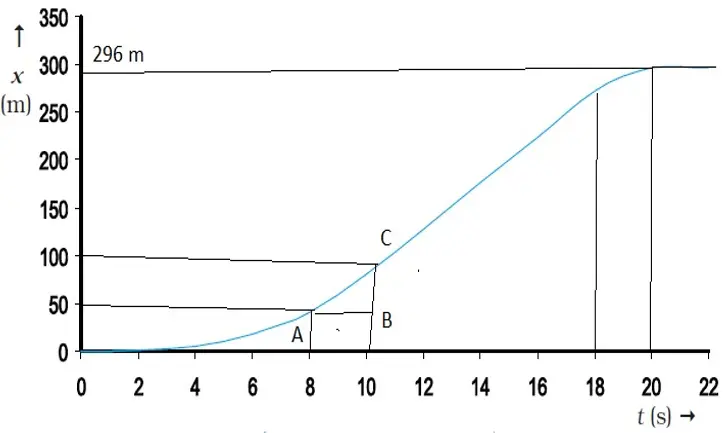
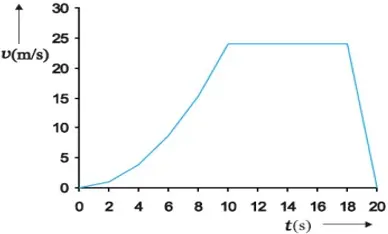
Position-time graph of a car

• The car starts from rest at time t = 0 s from the origin O and picks up speed till t = 10 s and thereafter moves with uniform speed till t = 18 s. Then the brakes are applied and the car stops att = 20 s and x = 296 m.

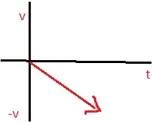
Position-time graph of an object moving with positive velocity

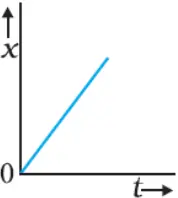
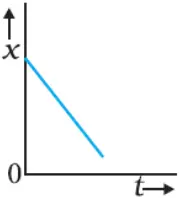
Position-time graph of an object moving with negative velocity

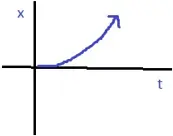
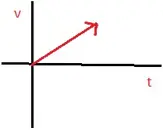
Position-time graph for motion with positive acceleration

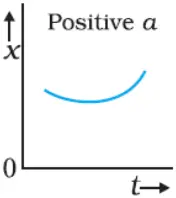
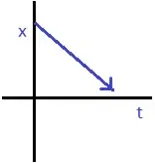
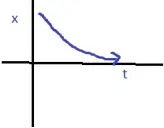
Position-time graph for motion with negative acceleration

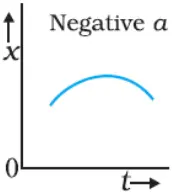
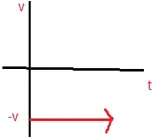
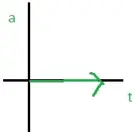
Position-time graph for motion with zero acceleration

PROBLEM-1

• Calculate the average velocity between 5s and 7s from the graph.

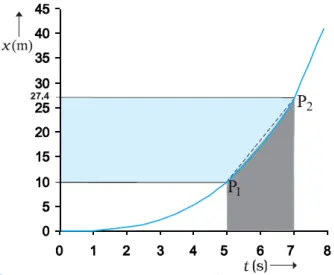
Solution

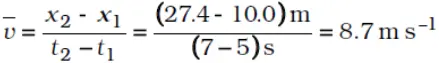
PROBLEM-2

A drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1 m long and requires 1 s. Plot the x-t graph of his motion. Determine graphically and otherwise how long the drunkard takes to fall in a pit 13 m away from the start.

Solution

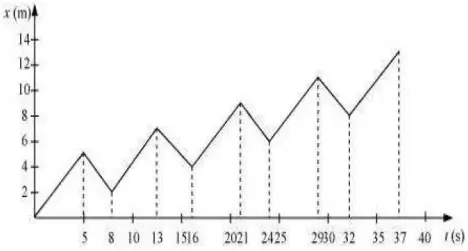
Time taken to fall in pit =37s.

VELOCITY – TIME GRAPH ( v-t GRAPH)

• A graph with velocity along Y –axis and time along X-axis.
• The acceleration at an instant is the slope of the tangent to the v–t curve at that instant.
• Area under the v-t graph gives the displacement.

Uses of v-t graph

• To find the displacement
• To find the velocity at any time
• To find the acceleration at any time
• To know the nature of motion

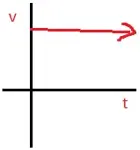
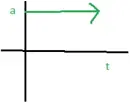
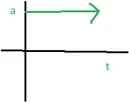
v-t graph of motion in positive direction with positive acceleration

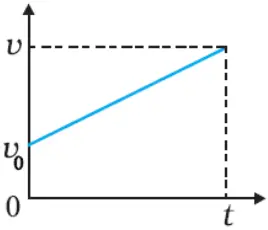
v-t graph of motion in positive direction with negative acceleration

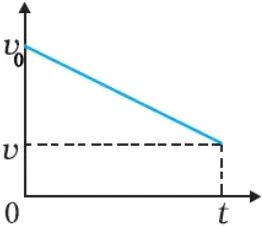
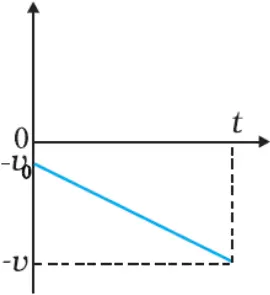
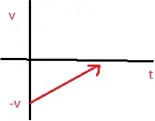
v-t graph of motion in negative direction with negative acceleration

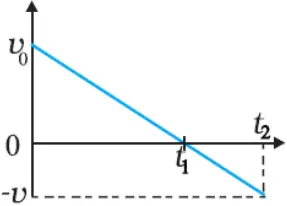
v-t graph of motion of an object with negative acceleration that changes direction at time t1.

PROBLEM-1

Draw v-t graph from the given x-t graph.

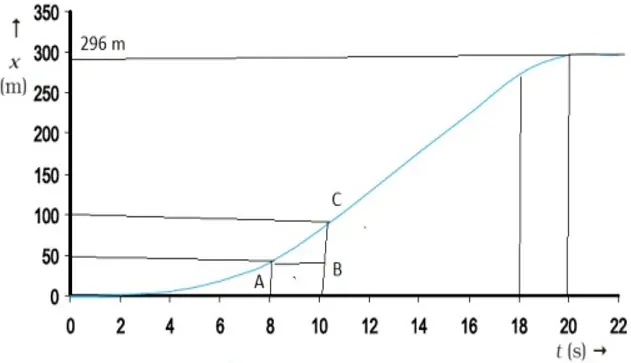
Solution

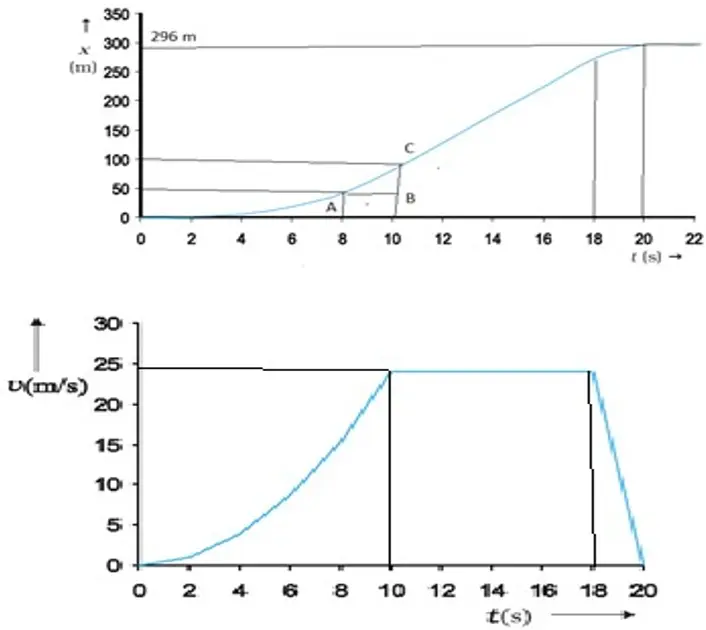
PROBLEM-2

• Velocity-time graph of a ball thrown vertically upwards with an initial velocity is shown in figure.

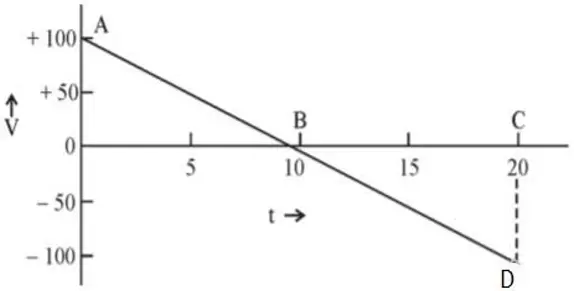
1. What is the magnitude of initial velocity of the ball?
2. Calculate the distance travelled by the ball during 20 s, from the graph.
3. Calculate the acceleration of the ball from the graph

Solution

1. 100 m/s
2. 
   

   

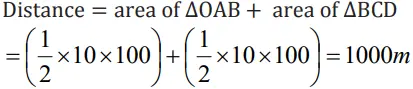
      3. Acceleration = slope of the graph

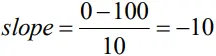
• Therefore acceleration = -10m/s²

ACCELERATION –TIME GRAPH

• A graph with acceleration along Y –axis and time along X-axis.
• Area under acceleration – time graph gives velocity.

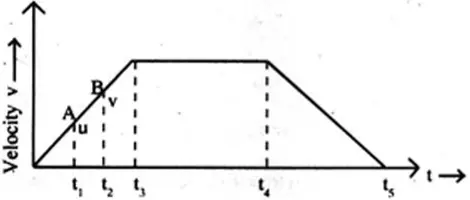
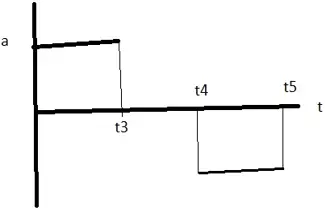
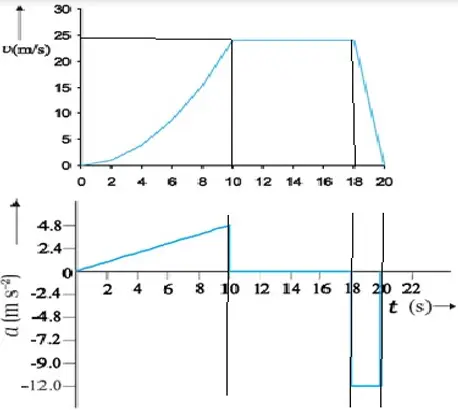
PROBLEM

• The graph shows the velocity – time graph of a moving body in a one dimensional motion. Draw the corresponding acceleration – time graph

Solution

PROBLEM -2

Draw acceleration –time graph from the velocity-time graph given below.

Solution

PROBLEM -3

which of these cannot possibly represent one-dimensional motion of a particle.

Solution

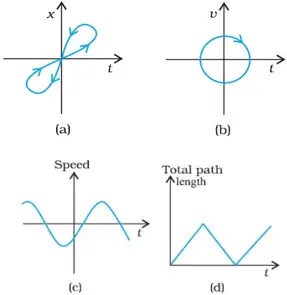
1. No – because a particle cannot have two positions at the same instant of time.
2. No – because particle can never have two values of velocities at the same instant of time.
3. No- speed cannot be negative
4. No – total path length cannot decrease with time.

NATURE OF GRAPHS IN A NUTSHELL

x-t Graph	v-t Graph	a-t Graph

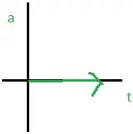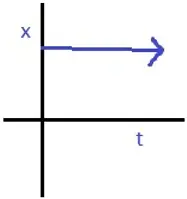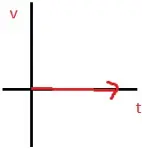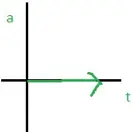KINEMATIC EQUATIONS FOR UNIFORMLY ACCELERATED MOTION

velocity–time graph of an object moving with uniform acceleration and with initial velocity v₀

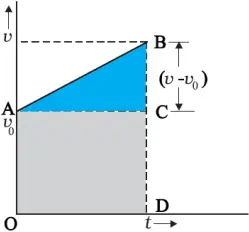
Velocity – Time Relation

• We have

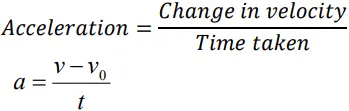
• Where v- final velocity, a – acceleration v₀ –initial velocity

at = v − v₀

Or v = v₀ + at

Displacement-Time Relation

• We know , area under v-t graph = Displacement
• Thus, the displacement at any time interval 0 and t, is given y

• 
  

  

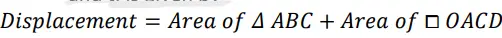
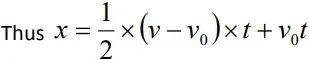
• But v − v₀ = at
• Thus

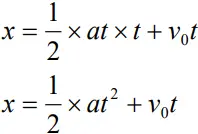
• Therefore

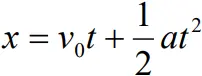
• If x_o is the initial displacement

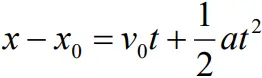
Velocity –Displacement Relation

• We have

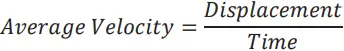
• Thus

Displacement = Average velocity x time

• Therefore

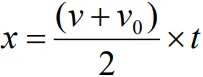
• But

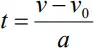
• Thus

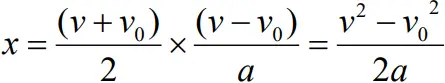
Therefore

v² = v₀² + 2ax

• If x_o is the initial displacement

v² = v₀² + 2a (x – x₀ )

Thus the equation of motion are

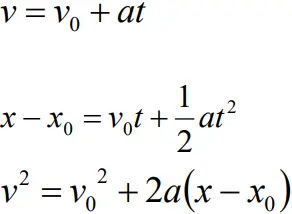
PROBLEM

• A ball is thrown vertically upwards with a velocity of 20 m s–1 from the top of a multistorey building. The height of the point from where the ball is thrown is 25.0 m from the ground.

a) How high will the ball rise ?

b) how long will it be before the ball hits the ground? Take g = 10 m/s²

Solution

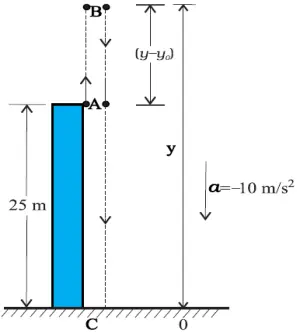
a) Given v₀ = +20 m/s , a = -g =10 m/s , v = 0

• Using the equation

v² = v₀² + 2a(y – y₀)

• We get

(y − y₀ ) = 20m

b). We have y₀ = 25 m, y = 0 m, v_o = 20 m /s, a = –10m /s²,

• Using the equation

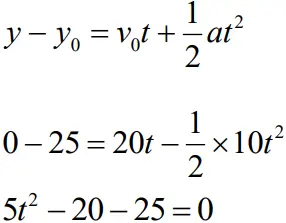
• Solving this quadratic equation we get, t=5s.

MOTION OF AN OBJECT UNDER FREE FALL

• A body falling under the influence of acceleration due to gravity alone is called free fall (air resistance neglected)
• If the height through which the object falls is small compared to the earth’s radius, g can be taken to be constant, equal to 9.8 m s–2.
• Free fall is an example of motion with uniform acceleration.
• Since the acceleration due to gravity is always downward, it is in the negative direction.
• Acceleration due to gravity = – g = – 9.8m/s2.

Equations of motion of a freely falling body

• For a freely falling body with v0=0 and y0 =0, the equations of motion are

Acceleration –Time graph of a freely falling body

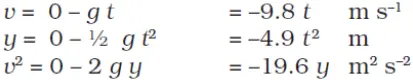
Velocity – Time graph of a freely falling body

Position –Time graph of a freely falling body

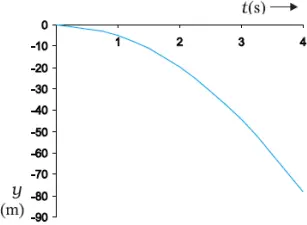
Galileo’s law of odd numbers

• The distances traversed, during equal intervals of time, by a body falling from rest, stand to one another in the same ratio as the odd numbers beginning with unity [namely, 1: 3: 5: 7……]

Proof

• Divide time interval of motion into equal intervals
• The distance travelled is found out using

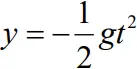
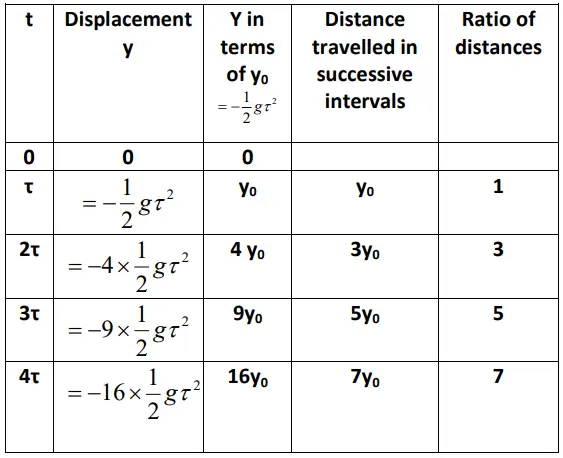
• Thus ratio of distances is found to be 1:3:5:7:…..

STOPPING DISTANCE OF VEHICLES

• When brakes are applied to a moving vehicle, the distance it travels before stopping is called stopping distance.
• Stopping distance is an important factor considered in setting speed limits, for example, in school zones
• Stopping distance depends on the initial velocity (v0) and the braking capacity, or deceleration (–a) that is caused by the braking.

Equation for Stopping Distance

• Let the distance travelled by the vehicle before it stops be, d.
• Substituting v=0 , x=d and acceleration = – a in the equation

 

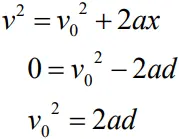
• Thus, stopping distance ,

• Thus stopping distance is proportional to square initial velocity.

REACTION TIME

• Reaction time is the time a person takes to observe, think and act.

• Dropping a ruler the reaction time can be calculated using the formula

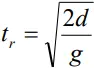
• Where d is the distance moved before the reaction.

RELATIVE VELOCITY

• It is the velocity measured whenever there is a relative motion between objects.
• The velocity of object B relative to object A is

v_BA = v_B – v_A

• Similarly, velocity of object A relative to object B is:

v_AB =v_A – v_B

• Thus, v_BA = -v_AB

Special cases:-

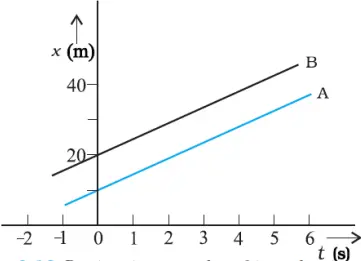
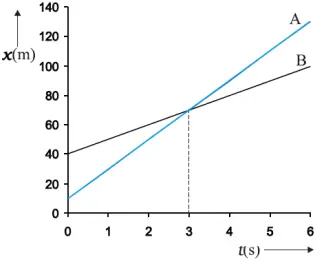
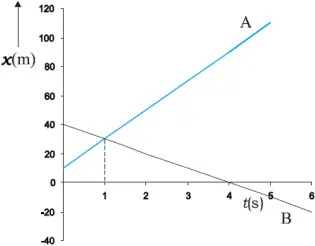
• If v_B = v_A, – relative velocity v_AB or v_BA is zero
• If v_A > v_B, v_B – v_A is negative, thus, object A overtakes object B at this time

Position-time graphs of two objects with equal velocities

Position-time graphs of two objects with unequal velocities

Position-time graphs of two objects with velocities in opposite directions

PROBLEM

Two parallel rail tracks run north south. Train A moves north with a speed of 54 km h–1, and train B moves south with a speed of 90 km h–1. What is the

1. Velocity of B with respect to A ?,
2. b) Velocity of ground with respect to B ?
3. c) velocity of a monkey running on the roof of the train A against its motion (with a velocity of 18 km h–1 with respect to the train A) as observed by a man standing on the ground ?

Solution