NCERT Notes For Class 11 Physics Chapter 4 Motion In A Plane

Class 11 Physics Chapter 4 Motion In A Plane

NCERT Notes For Class 11 Physics Chapter 4 Motion In A Plane, (Physics) exam are Students are taught thru NCERT books in some of state board and CBSE Schools.  As the chapter involves an end, there is an exercise provided to assist students prepare for evaluation.  Students need to clear up those exercises very well because the questions withinside the very last asked from those. 

Sometimes, students get stuck withinside the exercises and are not able to clear up all of the questions.  To assist students solve all of the questions and maintain their studies with out a doubt, we have provided step by step NCERT  Notes for the students for all classes.  These answers will similarly help students in scoring better marks with the assist of properly illustrated Notes as a way to similarly assist the students and answering the questions right.

NCERT Notes For Class 11 Physics Chapter 4 Motion In A Plane

Class 11 Physics Chapter 4 Motion In A Plane

 

MOTION IN A PLANE

SCALARS

• A scalar quantity is a quantity with magnitude only.
• It is specified by a single number, along with the proper unit.
• Examples are: the distance , mass, temperature time etc.
• Scalars can be added, subtracted, multiplied, and divided just as the ordinary numbers.
• Scalars can be added or subtracted with quantities with same units only. However, you can multiply and divide scalars of different units.

VECTORS

• A vector quantity is a quantity that has both a magnitude and a direction.
• A vector is specified by giving its magnitude by a number and its direction.
• Examples are displacement, velocity, acceleration and force.

Representation of Vectors

• Vectors are represented using a straight-line with an arrowhead.

• The length of the line is equal to or proportional to the magnitude of the vector and the arrowhead shows the direction.

TYPES OF VECTORS

Position Vectors

To describe the position of an object moving in a plane an arbitrary point is taken as origin.

A vector drawn from the origin to the point is known as position vector.

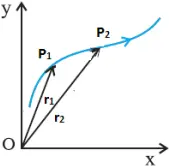
Displacement vectors

A vector joining the initial and final positions of an moving object is known as displacement vector.

The magnitude of the displacement vector is either less or equal to the path length of an object between two points

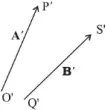
Equal vectors

• Two vectors A and B are said to be equal if, and only if ,they have the same magnitude and same direction.

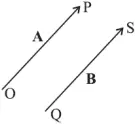
Unequal vectors

• Two vectors A and B are said to be unequal if, they have the different magnitude or direction.

Negative vector

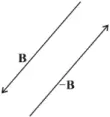
• Negative of a vector has the same magnitude but opposite direction.

Null vector ( Zero vector )

• A vector with zero magnitude and arbitrary direction
• Examples are :
  • Displacement of a stationary object
  • Velocity of a stationary object

Collinear vectors

• Vectors with same direction or opposite direction
• Their magnitudes may or may not be equal

Co-initial vectors

• Vectors having same initial point

Coplanar vectors

• Vectors lying on the same plane

UNIT VECTORS

• A vector with unit magnitude
• It is used to denote a direction
• Any vector can be represented as the product of its magnitude and a unit vector

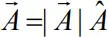
• Where Aˆ is unit vector
• Thus, unit vector,

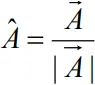
Orthogonal unit vectors

• Unit vectors along the x, y, z axes of a rectangular coordinate system is called orthogonal unit vectors.
• They are denoted as

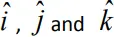
VECTOR ADDITION- GRAPHICAL METHOD

• The process of adding two or more vectors is called addition or composition of vectors.
• The result of adding two or more vectors is called resultant vector

Properties of vector addition

• Vector addition is commutative

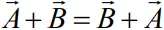
• Vector addition is associative

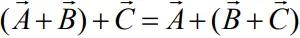
Vectors acting in the same direction – Addition

• The magnitude of the resultant of the vectors is the sum of the magnitudes of the vectors.
• The direction of the resultant vector is the same as that of the vectors added.

Vectors in opposite direction-subtraction

• The magnitude of the resultant vector is the difference of the magnitudes of the vectors.
• The direction of the resultant vector is the same as the direction of the vector with greater magnitude.
• We define the difference of two vectors A and B as the sum of two vectors A and –B

When two vectors are inclined at an angle (vectors in a plane)

• The two methods used are:

1. Triangle law of vectors
2. Parallelogram law of vectors

Triangle law of vectors

• If two vectors are represented in magnitude and direction by the two sides of a triangle taken in the same order, then third or closing side of the triangle taken in the opposite order represents the resultant in magnitude and direction.

Addition

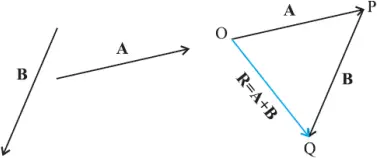
Subtraction

In subtraction the negative of the vector to be subtracted is added with the vector

Parallelogram law of vectors

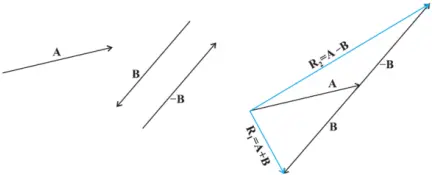
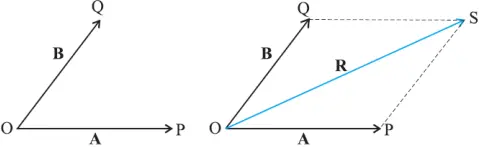
If two vectors can be represented in magnitude and direction by the two adjacent sides of a parallelogram drawn from a point, then the diagonal of the parallelogram drawn from that point represents the resultant in magnitude and direction.

VECTOR ADDITION – ANALYTICAL METHOD

Expression for the resultant of two vectors

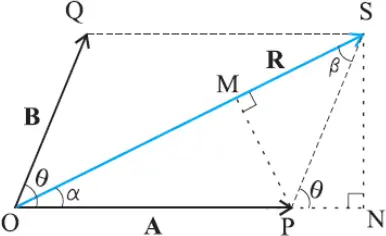
• Using the parallelogram method of vector addition, OS represents the resultant vector R

R = A + B

• SN is normal to OP and PM is normal to OS. From the geometry of the figure,

OS² = ON² + SN²

• But ON = OP + PN = A + Bcosθ and SN = Bsinθ
• Therefore

OS² = (A + Bcosθ)² + (Bsinθ)²

R² = A² + B² + 2ABcosθ

• Thus the magnitude of resultant is

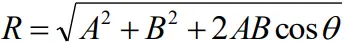
To find direction of resultant vector

• From the diagram,

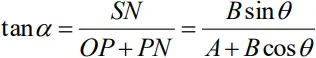
Law of sines

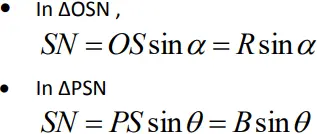
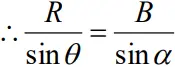
• Similarly

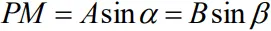
Or

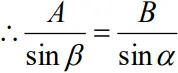
• Combining the two equations

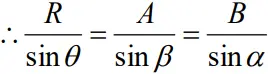
Special cases

(a) When A and B are in the same direction

R=A+B, the resultant is maximum and α=0, it is in the direction of A and B

(b) When A and B are perpendicular to each other

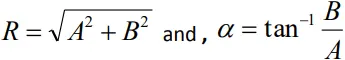
(c) When A and B are in opposite direction

R=A-B, the resultant is minimum and α=0, the resultant is in the direction of large vector.

PROBLEM-1

Rain is falling vertically with a speed of 35 m s^–1. Winds starts blowing after sometime with a speed of 12 m s^–1 in east to west direction. In which direction should a boy waiting at a bus stop hold his umbrella ?

Solution

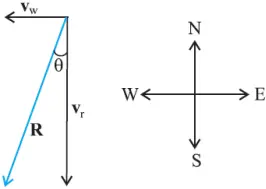
• The velocity of the rain and the wind are represented by the vectors v_r and v_w .
• Using the rule of vector addition, magnitude of the resultant R ,is

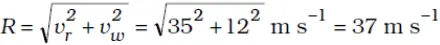
• The direction θ that R makes with the vertical is given by

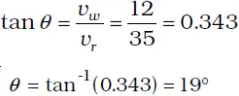
• Therefore, the boy should hold his umbrella at an angle of about 190 with the vertical plane towards the east.

PROBLEM-2

A motorboat is racing towards north at 25 km/h and the water current in that region is 10 km/h in the direction of 60° east of south. Find the resultant velocity of the boat.

Solution

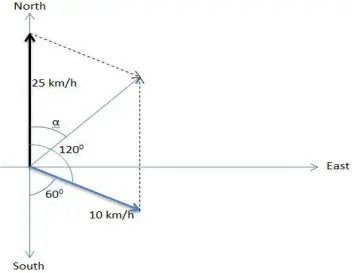
• The two velocities are at an angle of 1200.
• Thus, magnitude of resultant

R= √25² +10² +2 x 25 x 10 x cos120 = 21.8km/h

• The direction is

Multiplication of vectors by real numbers

• Multiplying a vector with a positive number λ gives a vector whose magnitude is changed by a factor λ but the direction is same as that of A.
• When multiplied with a negative number the direction reverses.

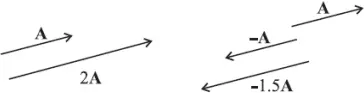
Resolution of Vectors

• Any vector in a plane can be represented as the resultant of two vectors.
• The splitting of a vector into its components is known as resolution of vectors.
• Thus, any vector A can be written as

Rectangular resolution

Any vector in a plane can be resolved into two components along x and y.

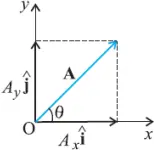
• Resolution of a vector in to two mutually perpendicular components in a plane is called rectangular resolution.
• Thus, in the form of components vector A can be written as

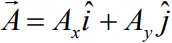
Resolution of vectors in three dimension

• In three dimensions any vector can be split up in to three components along x, y and z.

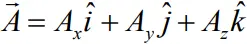
• The magnitude of vector A is

Position vector r in component form

• In three dimensions the position vector is given by

• where x, y, and z are the components of r along x-, y-, z-axes, respectively

Motion in a Plane

• The motion in a plane can be treated as two separate simultaneous one dimensional motion with constant acceleration along two perpendicular directions.

Position vector

• The position vector of an object in a plane is

Displacement vector

• Displacement vector of an object moving in a plane is

Average Velocity

• The average velocity is given by

The instantaneous velocity

• The instantaneous velocity is

• Thus

Average acceleration

• The average acceleration is given by

Instantaneous acceleration

• The acceleration at any instant is

• Thus

EQUATIONS OF MOTION IN A PLANE WITH CONSTANT ACCELERATION

Velocity –Time relation

Displacement –Time relation

RELATIVE VELOCITY IN TWO DIMENSIONS

PROBLEM

Rain is falling vertically with a speed of 35 m s^–1. A woman rides a bicycle with a speed of 12 m s^– 1 in east to west direction. What is the direction in which she should hold her umbrella?

Solution

• Since the woman is riding a bicycle, the velocity of rain as experienced by her is the velocity of rain relative to the velocity of the bicycle she is riding

• This relative velocity vector makes an angle  with the vertical, given by

• Thusθ= 19⁰
• Therefore, the woman should hold her umbrella at an angle of about 19° with the vertical towards the west.

PROJECTILE MOTION

• An object that is in flight after being thrown or projected is called a projectile.
• The horizontal component of velocity remains unchanged.
• Due gravity vertical component of velocity changes with time.
• It is assumed that air resistance has negligible effect on motion of the projectile.
• The trajectory or path of a projectile is parabola.

Motion of an object projected with velocity v0 at an angleθ

• After the object has been projected, the acceleration acting on it is that due to gravity which is directed vertically downward:

• The components of initial velocity v_o are :

• If we take the initial position to be the origin of the reference frame (x0=0 , y0=0), the equations of motion for the projectile is given by

Equation of path of a projectile

The parabolic path of a projectile

• At the highest point , velocity is zero, but still there is acceleration due to gravity.

Time of maximum height (t_m)

• At maximum height vy = 0,
• If t_m is the time of maximum height, then

Time of Flight of the projectile ( T )

• The total time during which the projectile is in flight is called time of flight .

Equation of Time of Flight

• During time of flight we have, the vertical displacement y=0,
• thus

Maximum Height of a Projectile (H)

• We have the vertical displacement,

• At maximum height y =H and t = tm , then

Horizontal Range of a Projectile (R)

• The horizontal distance travelled by the projectile during the time of flight is called horizontal range.
• R = Horizontal velocity x Time of flight

Maximum horizontal range

• Range is maximum when 2 = 900 or =450.
• Thus

PROBLEM -1

A hiker stands on the edge of a cliff 490 m above the ground and throws a stone horizontall with an initial speed of 15 m s^-1. Neglecting air resistance, find

1. the time taken by the stone to reach the ground.
2. the speed with which it hits the ground.

(Take g = 9.8 m s^-2 ).

Solution

• We choose the origin of the x-,and y axis at the edge of the cliff and t = 0 s at the instant the stone is thrown.

1. We have

• Here y₀ =0, v_0y =0, a_y = – g = 9.8 m/s ² and y = – 490 m, therefore

PROBLEM -2

• A cricket ball is thrown at a speed of 28 m s–1 in a direction 30° above the horizontal.

Calculate

1. the maximum height
2. the time taken by the ball to return to the same level
3. the distance from the thrower to the point where the ball returns to the same level.

Solution

1. The maximum height is

2g 29.8

UNIFORM CIRCULAR MOTION

• When an object follows a circular path at a constant speed, the motion of the object is called uniform circular motion.
• In uniform circular motion the magnitude of velocity of the particle remains constant, but the direction changes continuously.
• The velocity at any point is along the tangent to the path at that point.
• The acceleration directed towards the centre of the path of motion is called normal acceleration or radial acceleration or centripetal acceleration.

Angular Displacement (θ)

• The angle swept by the radius vector in a given time.
• It is a vector quantity and its unit is radian.

Angular velocity or Angular frequency (ω)

• It is the time rate of change of angular displacement.
• The average angular velocity

• The instantaneous angular velocity

• The S I unit is radian / second.

Time period ( T )

Time taken by the particle to complete one revolution.

Frequency (ν)

It is the number of revolutions made by the particle in one second.

Angular acceleration (α)

• It is the time rate of change of angular velocity.
• Average angular acceleration is

• The instantaneous angular acceleration is

• The S I unit of angular acceleration is rad/s2.

Relation connecting Angular Velocity and Linear Velocity

• If the distance travelled by the object during the time Δt is Δs ,the average velocity is

• From the diagram we have , Δs = RΔθ, R – radius

Relation between acceleration and angular acceleration

Velocity of uniform circular motion

• Magnitude of velocity is a constant.
• The velocity at any point is along the tangent to the path at that point.
• The change in velocity is directed towards the centre of the circular path.

Centripetal acceleration

• Acceleration experienced by an object undergoing uniform circular motion.
• Always directed towards the centre of the circle.
• Magnitude of the centripetal acceleration is a constant.
• The direction changes — pointing always towards the centre.

Equation for centripetal acceleration

• In the diagram the triangle CPP′ formed by the position vectors and the triangle GHI formed by the velocity vectors v, v′ and Δv are similar.
• Thus, ratio of the magnitudes of corresponding sides is given by

• Where R – radius of the circle

PROBLEM

An insect trapped in a circular groove of radius 12 cm moves along the groove steadily and completes 7 revolutions in 100 s.

(a) What is the angular speed, and the linear speed of the motion?

(b) Is the acceleration vector a constant vector ? What is its magnitude?

Solution