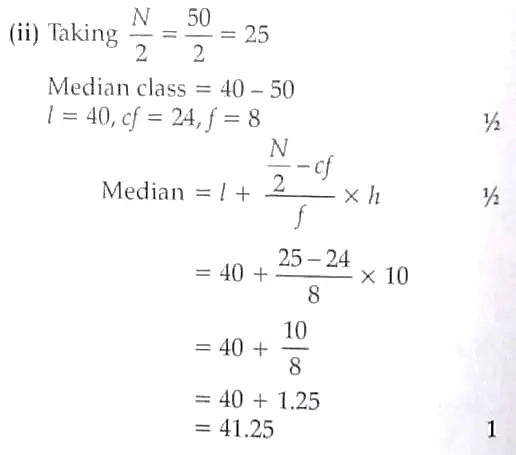Maths Basic Term 2 Sample Paper 2022 (Solved)

Class 10 Maths Basic Term 2 Sample Paper 2022, (Maths) exams are Students are taught thru NCERT books in some of the state board and CBSE Schools. As the chapter involves an end, there is an exercise provided to assist students to prepare for evaluation. Students need to clear up those exercises very well because the questions inside the very last asked from those.

Sometimes, students get stuck inside the exercises and are not able to clear up all of the questions. To assist students, solve all of the questions, and maintain their studies without a doubt, we have provided a step-by-step NCERT Sample Question Papers for the students for all classes. These answers will similarly help students in scoring better marks with the assist of properly illustrated Notes as a way to similarly assist the students and answer the questions right.

Class 10 Maths Standard Term 2 Sample Paper 2022

General Instructions:

1. The question paper consists of 14 questions divided into 3 sections A, B, C.

2. Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.

3. Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.

4. Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study based questions.

Section – A

[2 Marks each]

1. Find the nature of roots of the quadratic equation 2x² – 4x + 3 = 0.

2. A solid metallic cylinder of radius 3.5 cm and height 14 cm is melted and recast into a number of smaller solid metallic balls, each of radius 7/12 cm. Find the number of balls so formed.

OR

A cylindrical glass with diameter 15 cm has water to a height of 18 cm. A metal cube of 12 cm edge is immersed in it completely. Calculate the height by which water will rise in the cylinder.

3. Monthly expenditures on milk in 100 families of a housing society are given in the following frequency distribution:

Find the mode.

4. If the n^th terms of the A.P – 1,4, 9, 14, ……. is 129. Find the value of n.

5. Convert the following cumulative distribution to a frequency distribution:

6. In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = DQ = 3 cm, then find PC + PD.

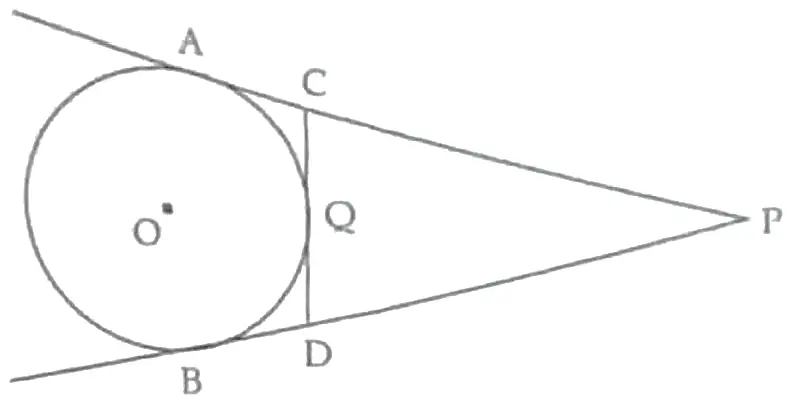
OR

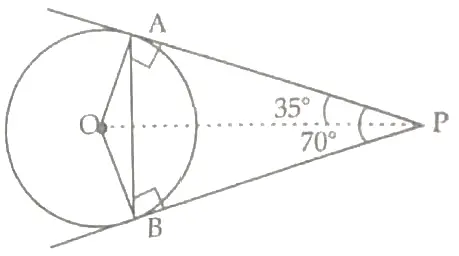
Two tangents PA and PB are drawn from an external point P to a circle inclined to each other at an angle of 70°, then what is the value of ∠PAB?

Section – B

[3 Marks Each]

7. Prove that the n^th term of an A.P. cannot be n² + 1. Justify your answer.

OR

If the n^th term of an A.P. is 7 – 3n, find the sum of twenty five terms.

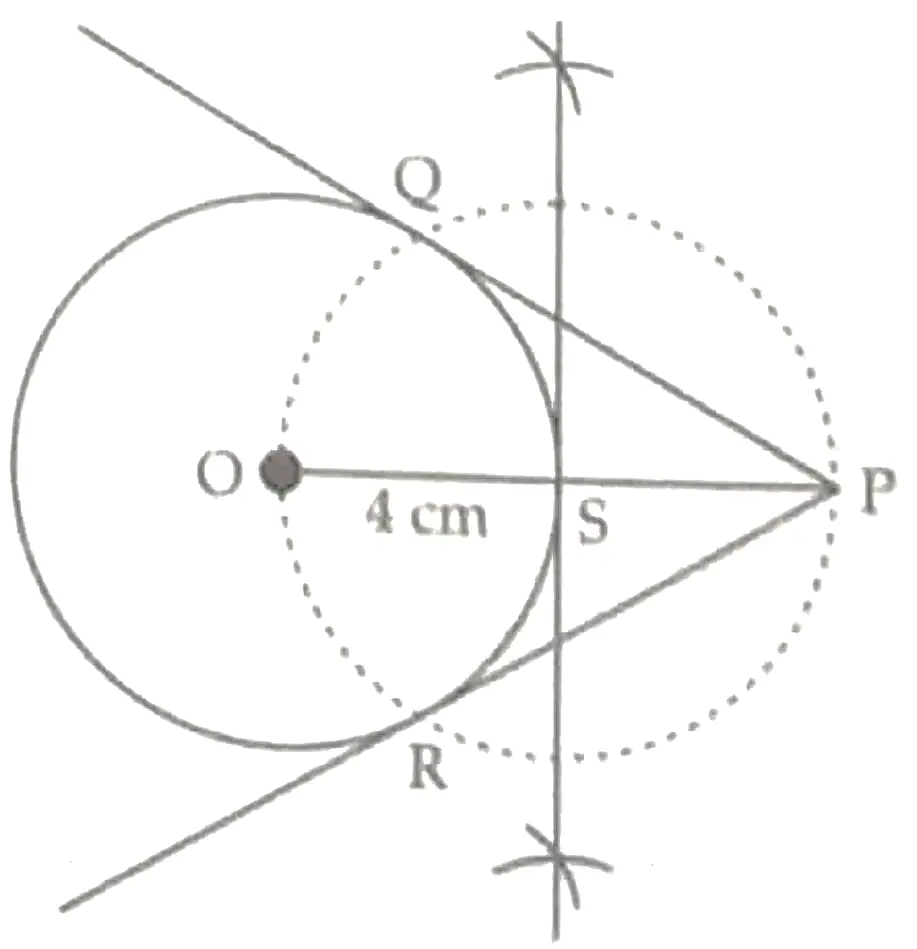
8. Construct a pair of tangents PQ and PR to a circle of radius 4 cm from a point P outside the circle 8 cm away from the centre. Measure PQ and PR.

9. If x = 2/3 and x = -3 are roots of the quadratic equation ax² + 7x + b = 0, find the values of a and b.

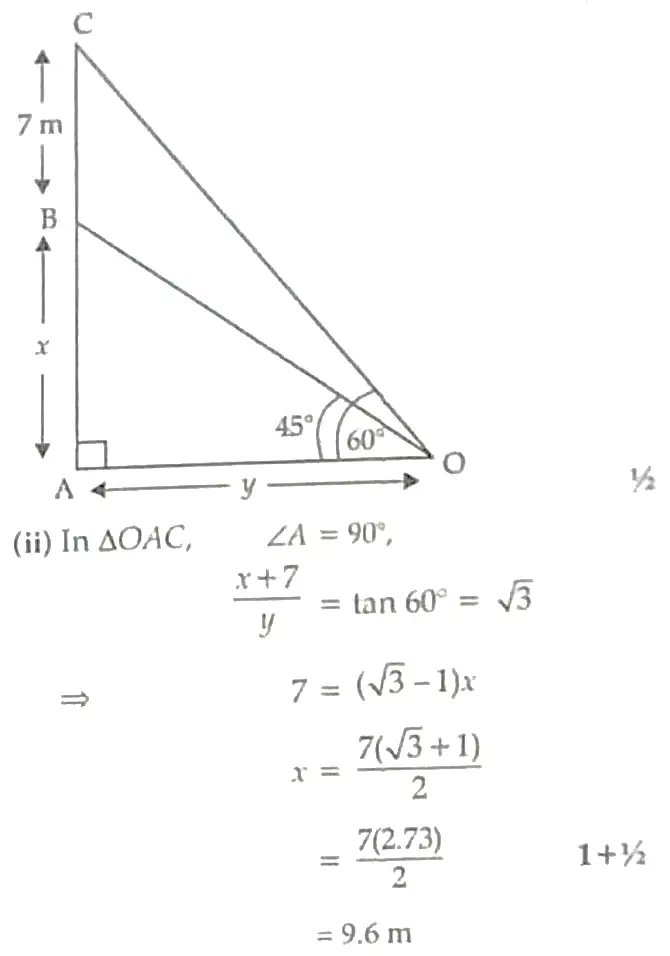
10. A 7 m long flagstaff is fixed on the top of a tower standing on the horizontal plane. From point on the ground, the angles of elevation of the top and bottom of the flagstaff are 60° and 45° respectively. Find the height of the tower correct upto one place of decimal. (Use √3 = 1.73)

Section – C

[4 Marks Each]

11. A copper rod of diameter 1 cm and length 8 cm is drawn in to a wire of length 18 m of uniform thickness. Find the thickness of wire.

OR

The radii of two cylinders are in the ratio 2:3 and their heights are in the ratio 5:3. Find the ratio of their volumes and curved surface areas.

12. Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.

Case Study – 1

13. A kite is flying at a height of 90m above the ground. The string attached to the kite is temporarily the to a point on the ground. The inclination of the string with the ground is 60°.

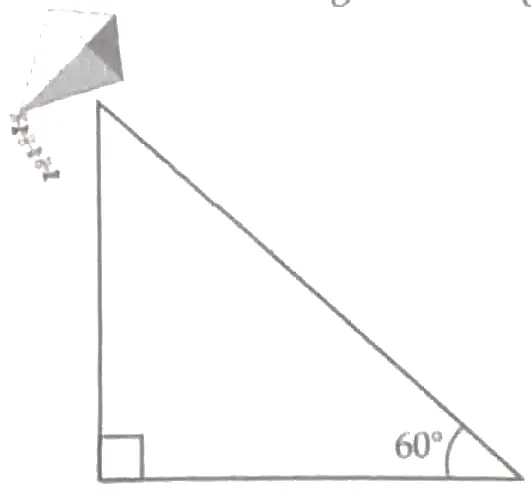
Based on above situation answer of the following questions:

(i) Find the length of the string. [Take √3 = 1.732)          [ 2 ]

(ii) If the inclination of the string with the ground is 30° then find the string.           [ 2 ]

Case Study – 2

14. A life insurance agent prepares a data of 50 policy holders according to their ages.

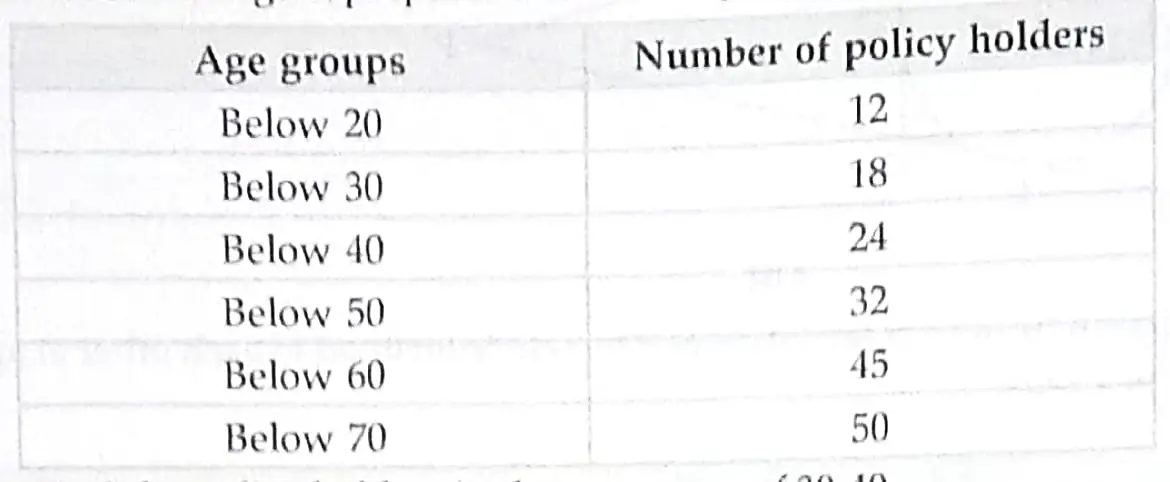
(i) Find the policy holders in the age group of 30-40.            [ 2 ]

(ii) Find the median of the above observation.             [ 2 ]

Solution of Sample Paper

Section – A

1. Given: 2x² – 4x + 3 = 0

On comparing above with ax² + bx + c = 0, we get

a = 2, b = -4 and c = 3

Now, D = b² – 4ac           1

= (-4)² – 4 × 2 × 3

= 16 – 24

= -8

Here, b² – 4ac < 0

Hence, the given equation has no real roots.           1

2. Let the number of recast balls be n

radius of cylinder R = 3.5 cm

height of cylinder h = 14 cm

radius of recast balls r = 7/12 cm

∴ Volume of n balls = Volume of cylinder

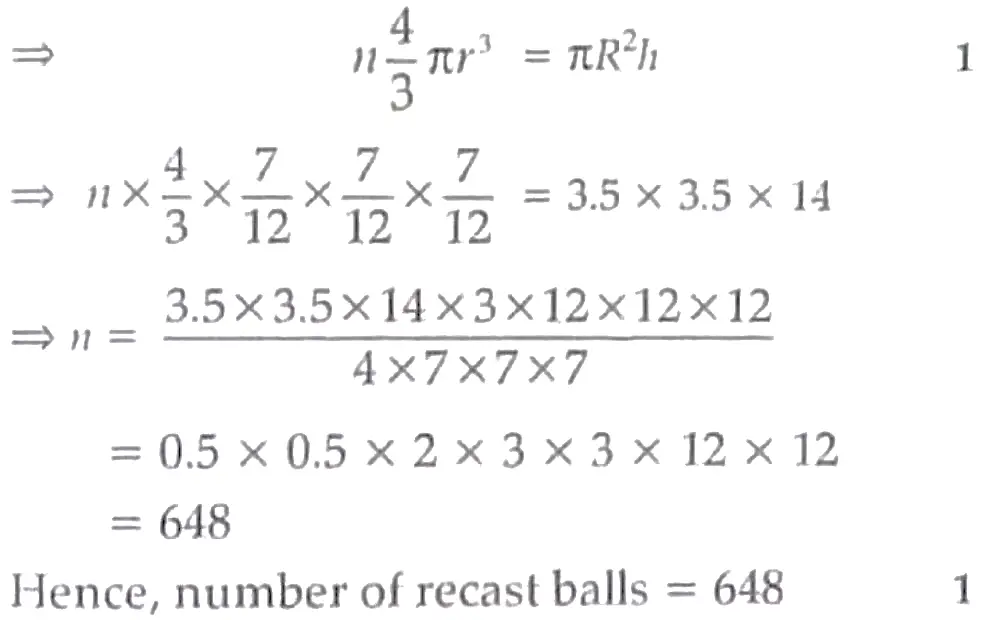
OR

Let the height of the cylindrical glass be h cm.

Radius of the cylindrical glass = 15/2 cm

Volume of water in the cylindrical glass

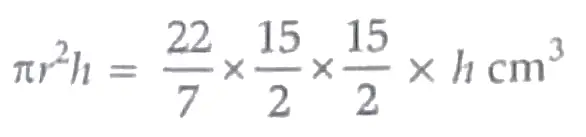           1

Volume of cube = Side³ = 12 x 12 x 12

Volume of water displaced in cylinder = Volume of cube

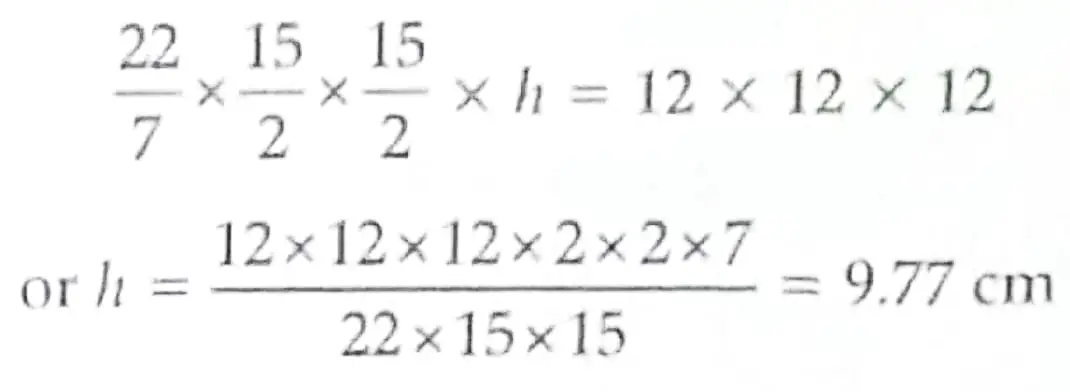          1

3. Modal class = 700-875. (Highest frequency class)

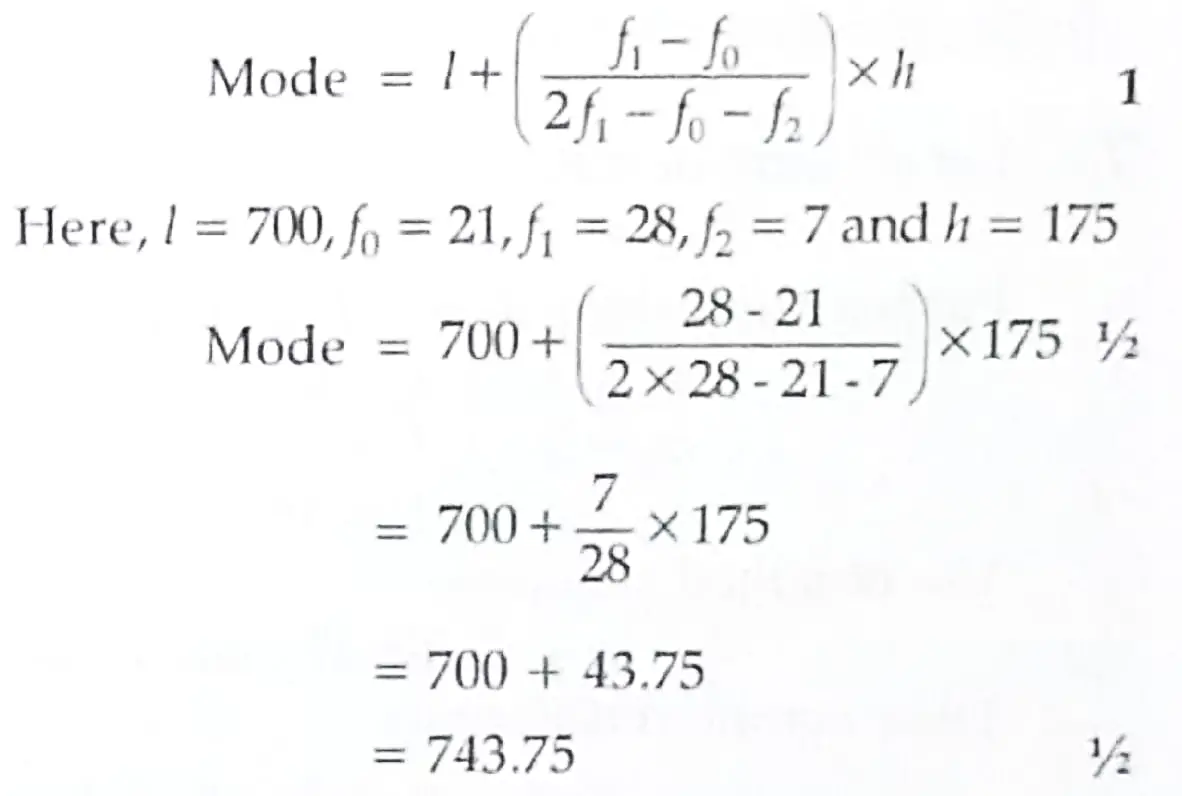
4. Given: first term (a) = -1

Common difference (d) = 4 – (-1) = 5

and a_n = 129

∴ a + (n – 1) d = 129 [Using formula of n^th term]

⇒ – 1 + (n – 1)5 = 129            1

⇒ 5(n – 1) = 130

⇒ n – 1 = 26

⇒ n = 27.            1

5.

              2

6. Here,

AC = CQ (Tangents from external point to a circle)

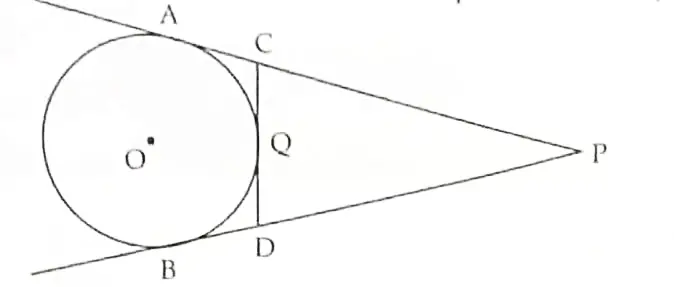
PA = PC + CA = PC + CQ (∴ CA = CQ)

⇒ 12 = PC + 3

⇒ PC = 12 – 3 = 9 cm            1

Similarly, PC = PD = 9 cm

∴ PC + PD = 9 + 9 = 18 cm.              1

OR

Sol. Here,

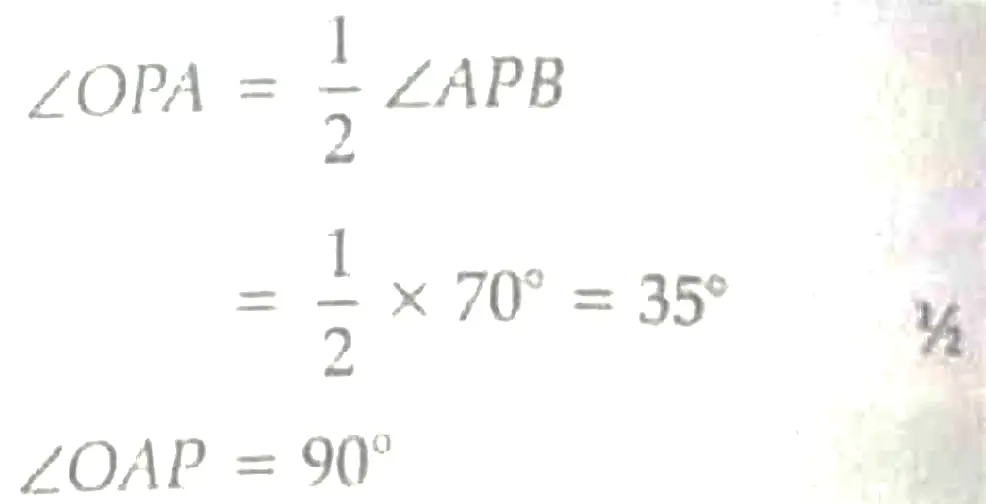
∴ ∠AOP = 180°- (90° + 35°) = 55° (Angle sum property)           ½

∠PAB = 180°- (90° + 35°)

= 55°          1

Section – B

7. Let n^th term of A.P.,

a_n = n² + 1

Putting the values of n = 1, 2, 3, ….., we get

a₁ = 1² + 1 = 2

a₂ = 2² + 1 = 5

a₃ = 3² + 1 = 10            1

The obtained sequence

= 2, 5, 10, 17,…….

Their common difference

=a₂ – a₁ = a₃ -a₂ = a₄ – a₃

or, 5 – 2 ≠ 10 – 5 ≠ 17 – 10

∴ 3 ≠ 5 ≠ 7           1

Since the common difference are not equal. Hence, n² + 1 is not a form of n^th term of an A.P.          1

OR

Sol. Here n = 25 and a_n = 7 – 3n

Taking n = 1, 2, 3, ….., we get

a₁ = 7 – 3 x 1 = 4

a₂ = 7 – 3 x 2 = 1

and a₃ = 7 – 3 x 3 = -2             1

∴ Given A.P. is 4, 1, -2,……

Here, a = 4 and d = 1 – 4 = -3               ½

Since,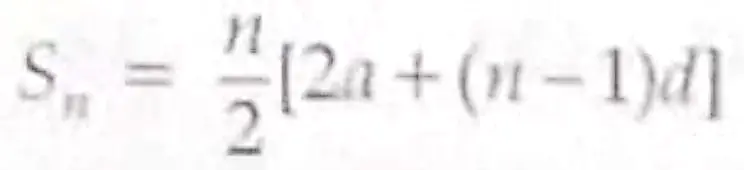

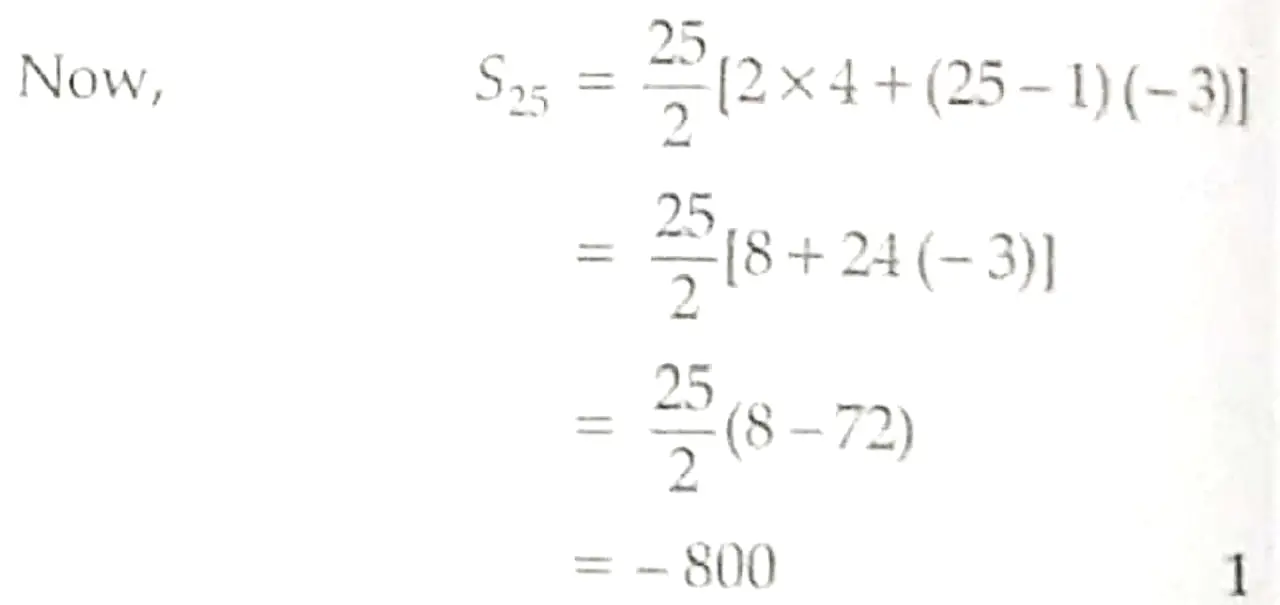
8. Steps of construction:

           2

1. Draw a line segment OP = 8 cm.

2. Taking O as centre and radius 4 cm, draw a circle.

3. Taking OP as diameter draw another circle which intersects the first circle at Q and R.

4. Join P to Q and P to R.

On measuring, we get PQ = PR = 6.93 cm            1

9. Substituting x = 2/3 in ax² + 7x + b = 0

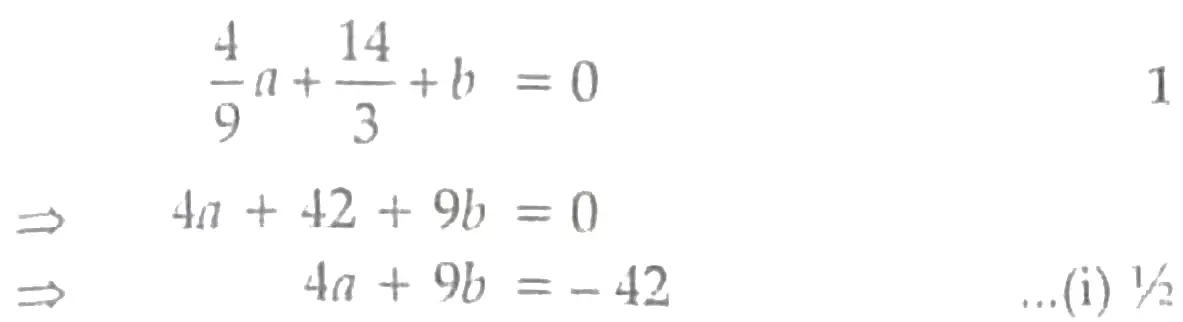
Again, substituting x = − 3 in ax² + 7x + b = 0

9a – 21 + b = 0           1

⇒ 9a + b = 21 …(ii)           ½

Solving (i) and (ii), we get

a = 3 and b = -6              1

10. (i) In ΔΟΑΒ, ∠A = 90°,

x/y = tan 45° = 1

⇒ x = y           1

Section – C

11. Diameter of copper rod, D = 1 cm

Radius of copper rod, R = 1/2 cm

Length of copper rod, I = 8 cm

Length of drawn wire, L = 18 m = 1800 cm           1

Since copper rod is drawn into wire of uniform thickness.

∴ Volume of wire = Volume of copper rod.

πr²L = πR²l [r = Radius of drawn wire]           1

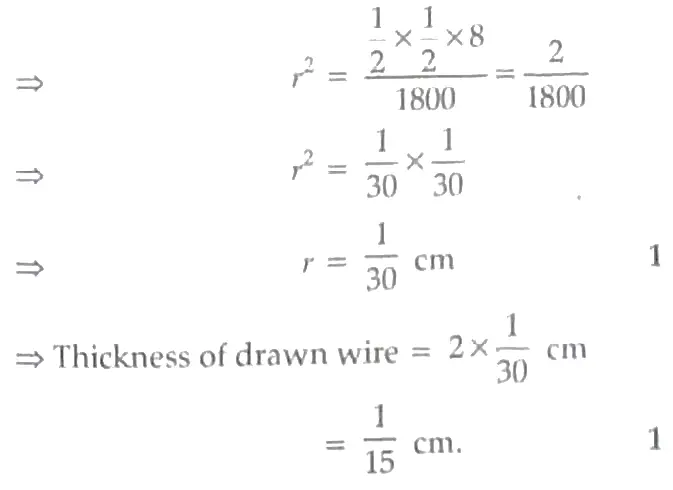
OR

Let the radius of 1^st sphere = r and height of first sphere = h cm.

Let the radius of 2^nd sphere = R and height = H

According to the question,

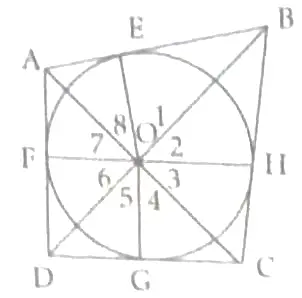
12. Given: A circle with centre O is inscribed in a quadrilateral ABCD.

In △AEO and △AFO,

OE = OF (radii of circle)

∠OEA = ∠OFA = 90° (radius is ⊥ to tangent)

AE = AF (tangent of a circle)

△AEO ≅ △AFO (SAS congruency)

∠7 = ∠8 …..(i) (CPCT)

         1

Similarly,

∠1 = ∠2 ….(ii)

∠3 = ∠4 …..(iii)

∠5 = ∠6 …(iv)         1

∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360°         1

(angle around a point is 360°)

2∠1 +2∠8 +2∠4 +2∠5 = 360°

∠1+∠8+ ∠4 + ∠5 = 180°

(∠1+∠8) + (∠4 + ∠5) = 180°

∠AOB + ∠COD = 180°        1

Hence Proved.

Case Study – 1

13. (i) Let ABC be a right angle triangle at ∠B = 90°

In △ABC,

Hence, the length of the string is 104 m approx.           1

(ii) Let ABC be a right angle triangle at ∠B = 90°

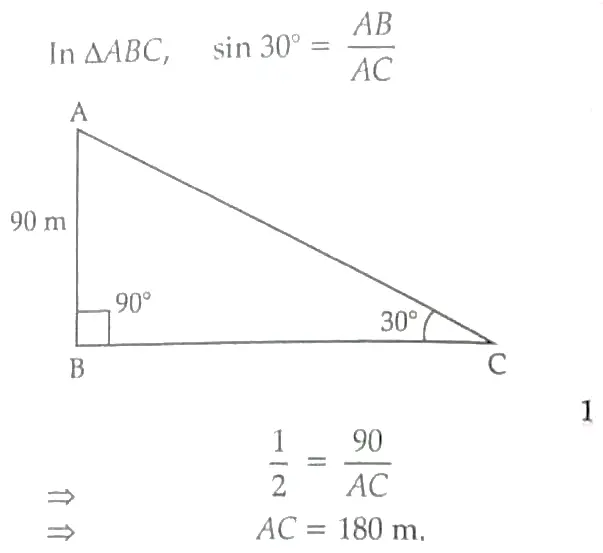
Hence, the length of the string is 180 m.        1

Case Study – 2

14. (i)

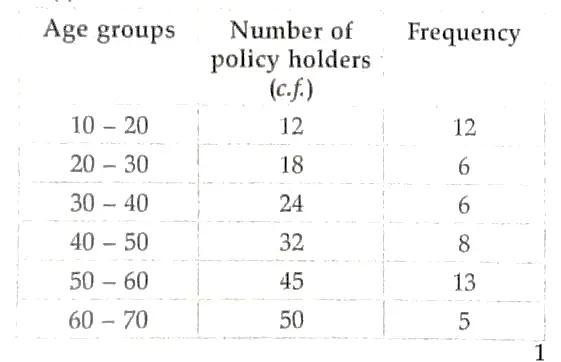
There are 6 Policy holders in the age group of 30-40.         1