Maths Basic Term 2 Sample Paper 2022 (Unsolved)

Class 10 Maths Basic Term 2 Sample Paper 2022, (Maths) exams are Students are taught thru NCERT books in some of the state board and CBSE Schools. As the chapter involves an end, there is an exercise provided to assist students to prepare for evaluation. Students need to clear up those exercises very well because the questions inside the very last asked from those.

Sometimes, students get stuck inside the exercises and are not able to clear up all of the questions. To assist students, solve all of the questions, and maintain their studies without a doubt, we have provided a step-by-step NCERT Sample Question Papers for the students for all classes. These answers will similarly help students in scoring better marks with the assist of properly illustrated Notes as a way to similarly assist the students and answer the questions right.

Class 10 Maths Basic Term 2 Sample Paper 2022

General Instructions:

1. The question paper consists of 14 questions divided into 3 sections A, B, C.

2. Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.

3. Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.

4. Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study based questions.

Section – A

[2 Marks each]

1. Solve for

2. Find the mode of the following distribution.

3. If x = 2/3 and x = -3 are roots of the quadratic equation ax² + 7x + b = 0, find the values of a and b.

4. Which term of the progression 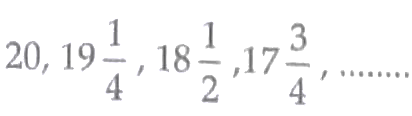is the first negative term?

OR

If k + 1, 3k and 4k + 2 be any three consecutive terms of an A.P then find k.

5. In a frequency distribution , if a = assumed mean = 55 , Σf_i = 100 and Σf_id_i = -300 , then find the mean of the distribution .

6. An isosceles triangle ABC, with AB = AC, circumscribes a circle, touching BC at P, AC at Q and AB at R. Prove that the contact point P bisects BC.

OR

Prove that the tangents drawn at the ends of a diameter of a circle are parallel.

Section – B

[3 Marks Each]

7. An electric pole is 12 m high. A steel wire tied to top of the pole is affixed at a point on the ground to keep the pole upright. If the wire makes an angle of 60° with the horizontal through the foot of the pole find the length of the wire.

OR

The horizontal distance between two towers is 60 m. The angle of elevation of the top of the taller tower as seen from the top of the shorter one is 30°. If the height of the taller tower is 150 m, then find the height of the shorter tower.

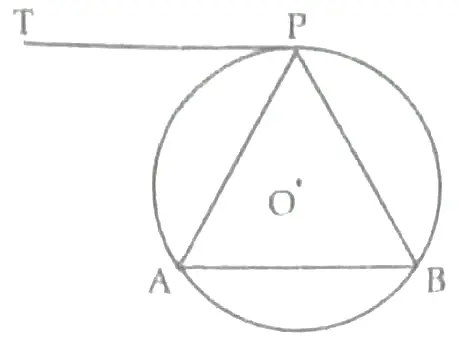
8. A tangent PT is drawn parallel to a chord AB of a circle as shown in the figure. Prove that APB is an isosceles triangle.

9. Marbles of diameter 1.4 cm are dropped into a cylindrical beaker of radius 7 cm containing some water. How many marbles must be dropped so that the water in the beaker rises by 28 cm.

10. Water is flowing at the rate of 30 km/h through a pipe of diameter 28 cm into a cuboidal pond which is 100 m long and 22 m wide. In what time the level of water in pond rises by 21 cm.

Section – C

[4 Marks Each]

11. Draw two concentric circles of radii 2 cm and 5 cm. Take a point P on the outer circle and construct a pair of tangents PA and PB to the smaller circle. Measure PA.

12. The table below shows the daily expenditure on food of 25 households in a locality. Find the mean daily expenditure on food.

OR

The mean of the following distribution is 18. Find the frequency f of the class 19-21.

Case Study – 1

13. A number of bricks were placed in the following manner,

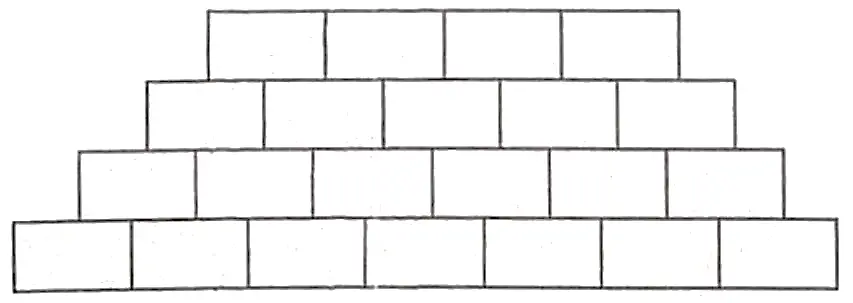
4 bricks in first row, 5 bricks in second row, and so on..

(i) How many rows will be formed for 165 bricks?        [ 2 ]

(ii) The A.P so formed, find the n^th term.          [ 2 ]

Case Study – 2

14. An electrician wants to repair wires with fault on a pole of height 10 m. He wants to reach a point 8 m below the top of the pole to repair the wires.

(i) He places the ladder at point where the angle between the ladder and ground is 60°. Find the distance of the point from the pole.          [ 2 ]

(ii) Find the length of ladder.           [ 2 ]