Maths Basic Term 2 Sample Paper 2022 (Unsolved)

Class 10 Maths Basic Term 2 Sample Paper 2022, (Maths) exams are Students are taught thru NCERT books in some of the state board and CBSE Schools. As the chapter involves an end, there is an exercise provided to assist students to prepare for evaluation. Students need to clear up those exercises very well because the questions inside the very last asked from those.

Sometimes, students get stuck inside the exercises and are not able to clear up all of the questions. To assist students, solve all of the questions, and maintain their studies without a doubt, we have provided a step-by-step NCERT Sample Question Papers for the students for all classes. These answers will similarly help students in scoring better marks with the assist of properly illustrated Notes as a way to similarly assist the students and answer the questions right.

Class 10 Maths Basic Term 2 Sample Paper 2022

General Instructions:

1. The question paper consists of 14 questions divided into 3 sections A, B, C.

2. Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.

3. Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.

4. Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study based questions.

Section – A

[2 Marks each]

1. Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of larger circle which touches the smaller circle.

OR

A circle is inscribed in a △ABC touching AB, BC and AC at P, Q, and R respectively, If AB = 10 cm, AR = 7 cm and CR = 5 cm, then find the length of BC.

2. Two cubes have their volumes in the ratio 1 : 64. Find the ratio of their surface areas.

OR

Find the height of a cylinder whose radius is 7 cm and the total surface area is 968 cm² .

3.

Based on above distribution answer the following questions.

(a) Find the median class

(b) Find the sum of lower limit of modal class and upper limit of median class.

4. Find the mean of the following data.

5. The tops of two towers of height x and y, standing on the ground, subtend the angles of 45° and 60° respectively at the centre of the line joining their feet, then find x : y.

6. A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string assuming that there is no slack in the string. [Take √3 = 1.732]

Section – B

[3 Marks Each]

7. Solve for x :

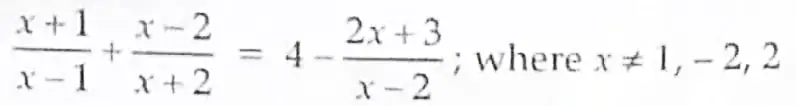
8. Determine an A.P whose third term is 9 and when fifth term is subtracted from 8^th term, we get 6.

OR

Find the number of all three-digit natural numbers which are divisible by 9.

9. A man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of hill as 30°. Find the distance of the hill from the ship and the height of the hill.

10. In the given figure, PQ is a chord of the circle with centre O and PT is a tangent. If ∠QPT – 60°, find ∠PRQ .

Section – C

[4 Marks Each]

11. Draw a line segment 10 cm long and divide it into three parts in the ratio 1 : 2 : 3 using ruler and compass.

12. Find the mean of the following distribution:

OR

The median of following frequency distribution is 32.5. Find the values of f₁ and f₂

Case Study – 1

13. A shopkeeper is trying to make a new type of toy shaped in the form of a hemisphere surmounted by a cone of same radius.

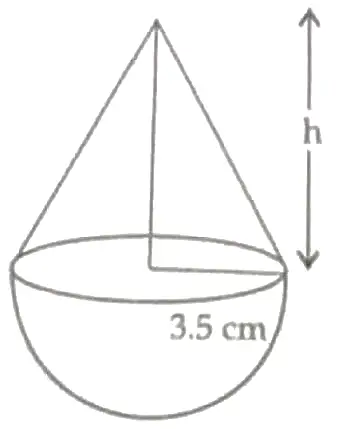
Based on above situation answer the following questions:

(i) If the radius of the toy is 3.5 cm and the total wood he has for making the toy is 166 ⅚ cm³. Find the height of the toy.       [ 2 ]

(ii) Find the cost of painting the hemispherical part at the rate of ₹ 12 per m².         [ 2 ]

Case Study – 2

14. Two pipes are filling a tank in 11 (1/9) minutes. One of the pipes takes 5 minutes more than the first pipe to fill the tank separately.

(i) Represent the above situation in the form of algebraic expression.           [ 2 ]

(ii) Find the time taken by each pipe to fill the tank separately.        [ 2 ]