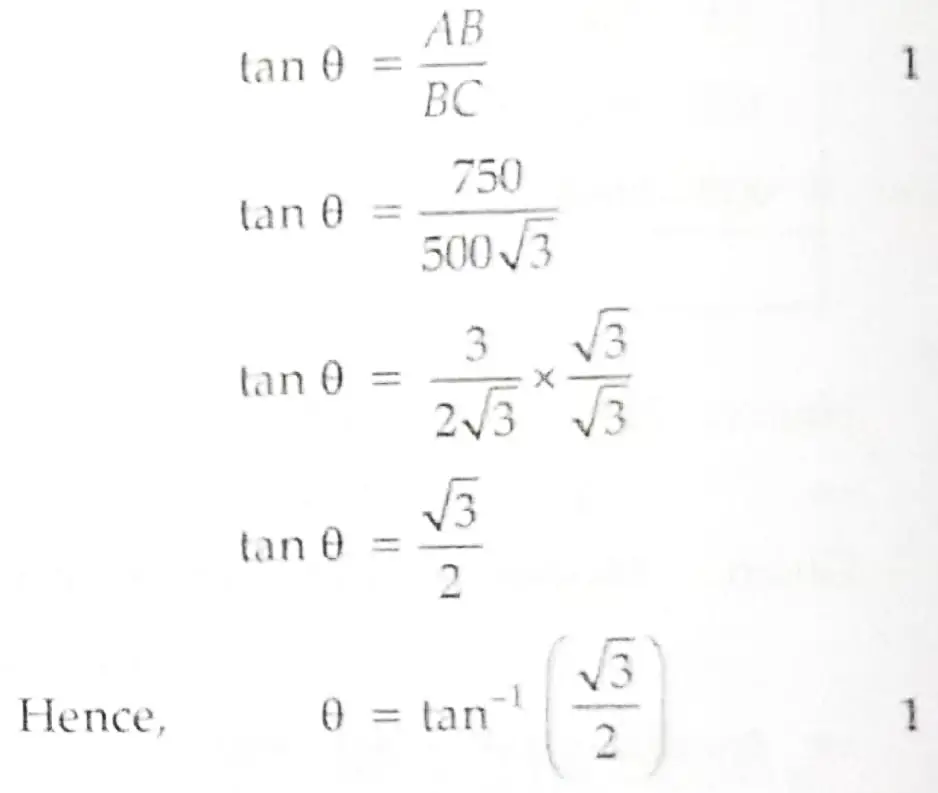Maths Basic Term 2 Sample Paper 2022 (Solved)

Class 10 Maths Basic Term 2 Sample Paper 2022, (Maths) exams are Students are taught thru NCERT books in some of the state board and CBSE Schools. As the chapter involves an end, there is an exercise provided to assist students to prepare for evaluation. Students need to clear up those exercises very well because the questions inside the very last asked from those.

Sometimes, students get stuck inside the exercises and are not able to clear up all of the questions. To assist students, solve all of the questions, and maintain their studies without a doubt, we have provided a step-by-step NCERT Sample Question Papers for the students for all classes. These answers will similarly help students in scoring better marks with the assist of properly illustrated Notes as a way to similarly assist the students and answer the questions right.

Class 10 Maths Basic Term 2 Sample Paper 2022

General Instructions:

1. The question paper consists of 14 questions divided into 3 sections A, B, C.

2. Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.

3. Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.

4. Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study based questions.

Section – A

[2 Marks each]

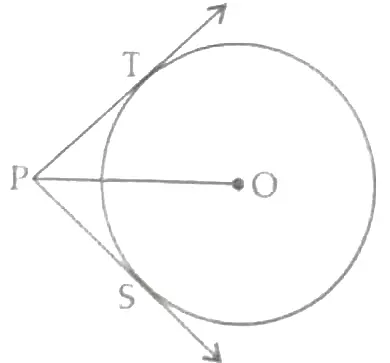
1. In the given figure, from a point P, two tangents PT and PS are drawn to a circle with centre O such that ∠SPT = 120°, prove that OP = 2PS.

OR

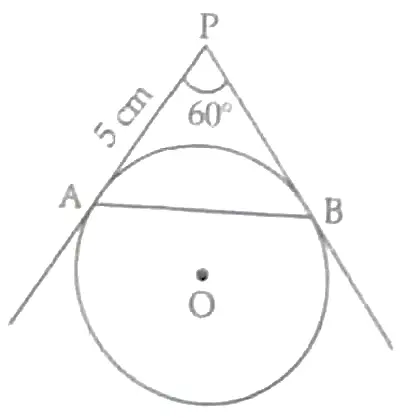
In Fig., AP and BP are tangents to a circle with centre O, such that AP = 5 cm and ∠APB = 60°. Find the length of chord AB.

2. A spherical ball of radius 6 cm is melted and re-casted into 3 spherical balls of equal dimensions, find the radius of the new spherical balls.

OR

Find the length of the cylindrical wire of radius 2 meters, which is drawn through 6 cubic meters of copper

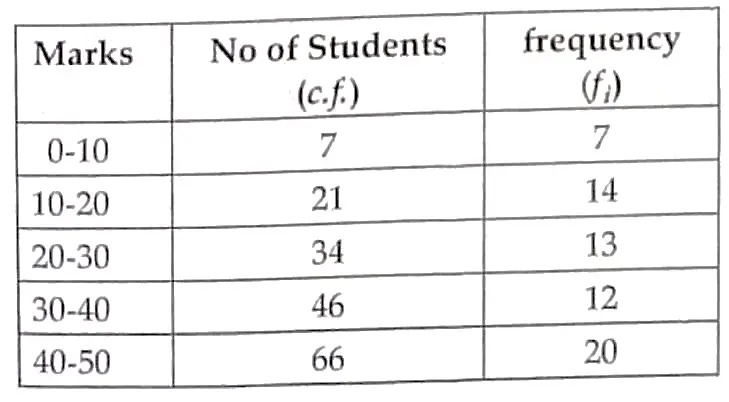
3. Find the mean of the following distribution.

4. (a) What are the measures of central tendency?

(b) If mean = 145.20 and median 138.57. Find mode.

5. Divide 27 into two parts such that the sum of their reciprocals is 3/20

6. A kite is flying at a height of 108 meters from the ground level, attached to a string inclined at 60° to the vertical. Find the length of the string to the nearest meter.

Section – B

[3 Marks Each]

7. If first term of an A.P. is 5 and last term is 45. Also the sum of all its term is 400. Find the number of terms and common difference of the A.P.

8. Find three consecutive odd positive integers, if the sum of whose squares is 371.

9. A vertical tower stands on a horizontal place and is surmounted by a vertical flag staff. At a point on the place 90 meters away from the tower observers the angles of elevation of the top and bottom of the flag-staff are respectively 30° and 45°. Find the height of the flag staff and that of the tower.

OR

An electric pole is 21 m high. A steel wire tied to top of the pole is affixed at a point on the ground to keep the pole up right. If the wire makes an angle of 60° with the horizontal through the foot of the pole, find the length of the wire.

10. Draw a circle of radius 3.5 cm. Draw two tangents to the circle such that they are inclined to each other at an angle of 120°.

Section – C

[4 Marks Each]

11. The median of the following data is 525. Find the values of x and y if the total frequency is 100.

OR

The following distribution table shows the marks obtained by 100 students of class X in a school during a particular academic session. Find the mode of this distribution.

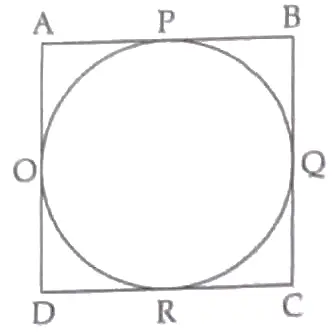
12. Prove that the rectangle which circumscribes a circle is a square.

Case Study – 1

13. A carpenter made a wooden a pen stand. It is in the shape of cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 12 cm x 8 cm x 4.5 cm. The radius of each of the depressions is 0.6 cm and the depth is 2.1 cm.

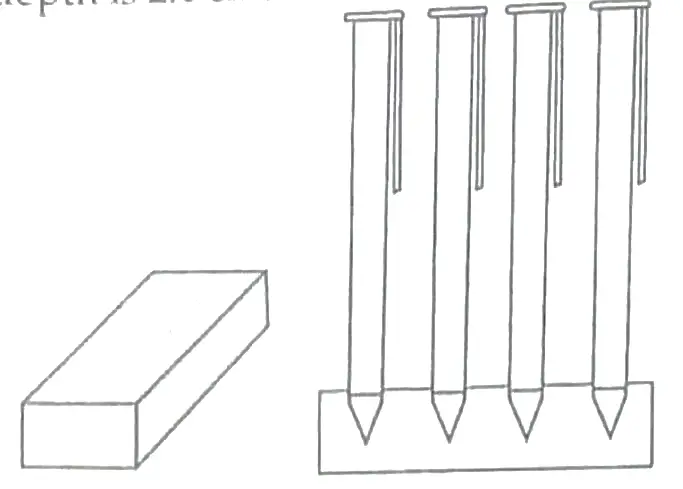
Based on above informations answer the following questions:

(i) What is volume of cuboid?           [ 2 ]

(ii) What is the volume of conical depression?          [ 2 ]

Case Study – 2

14. According to Air Delhi (Private airline) has upgraded its technology in last few years. With those upgradations the officials can find features of flight distance, speed and distance. The wind plays a vital role, when a flight will travel.

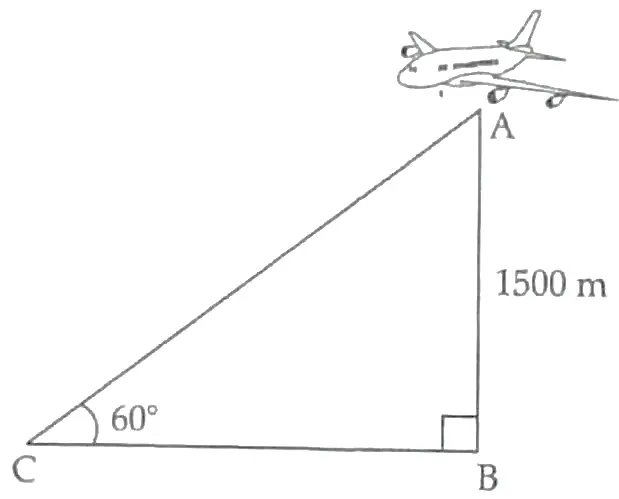
Based on above situation, answer the following questions:

(i) Find the length of BC in the above figure.          [ 2 ]

(ii) If the height at which the plane is flying is 750 m. Find the angle of elevation from the same point C. (Considering BC same as (A) part).         [ 2 ]

Solution of Sample Paper

Section – A

1. Given that ∠SPT = 120°

or, ∠OPS = 120° / 2 = 60°

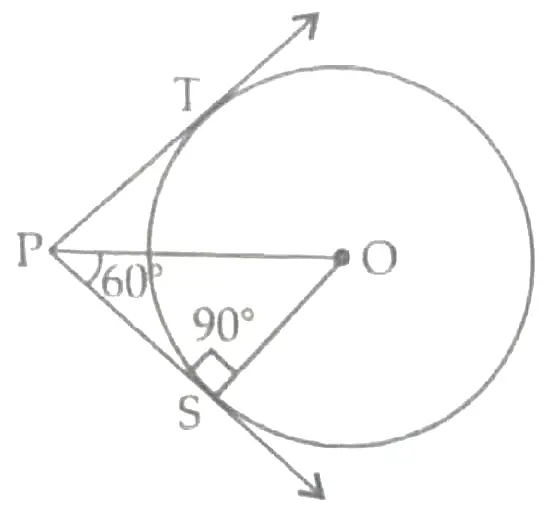       (as OP bisects ZSPT)        ½

Also, ∠PSO = 90° (as radius ⊥ tangent)          ½

∴ In right triangle POS,

cos 60° = PS/OP

or, 1/2 = PS/OP

or, OP = 2PS. Hence Proved.       1

Let the length of cylindrical wire be h the

OR

Given, PA = PB          ½

or, ∠PAB= ∠PBA = 60°       ½

∴ APAB is an equilateral triangle.       ½

Hence, AB = PA = 5 cm.          ½

Detailed Solution:

Given, AP and BP are tangents with centre O.

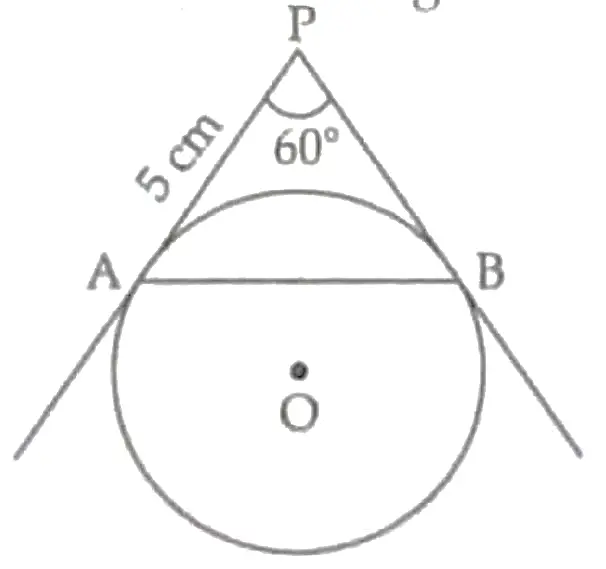        ½

Given AP = 5 cm

∴ AP = BP = 5 cm

(∴ Tangents are equal from external point P)

In ΔΑΡΒ,

∠ PAB = ∠PBA (Isosceles property)

∴ ∠PAB + ∠PBA + ∠APB = 180° (Angle sum property of a triangle)

⇒ 2 ∠PAB+ 60° = 180°

⇒ ∠PAB = 60°

i.e., ∠PAB= ∠PBA = ∠APB (each 60°)         ½

So, △APB is an equilateral triangle.

∴ AP = BP = AB = 5 cm (Sides are equation in an equilateral triangle)

Hence, the length of chord AB is 5 cm.           1

2. Volume of spherical ball of radius 6 cm = 3 x volume of spherical balls of radius ‘r’ cm

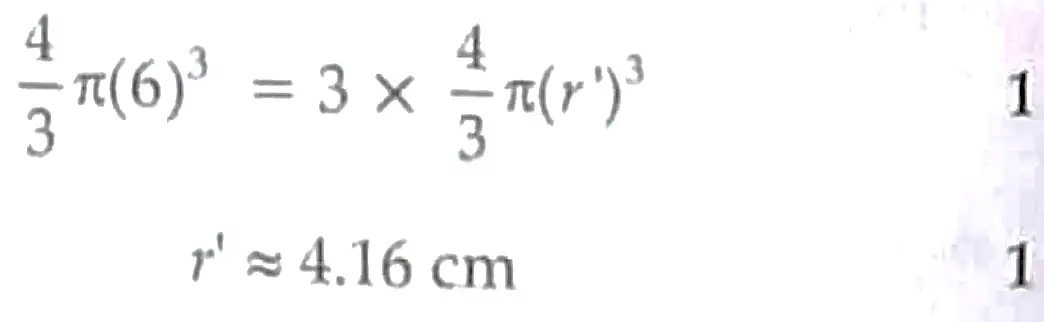
OR

Given, volume of copper = 6 m³

Radius of cylindrical wire (r) = 2 m

Volume of copper = Volume of cylindrical wire           1

6 m³ = π(2)²h

h = 0.48 m        1

3.

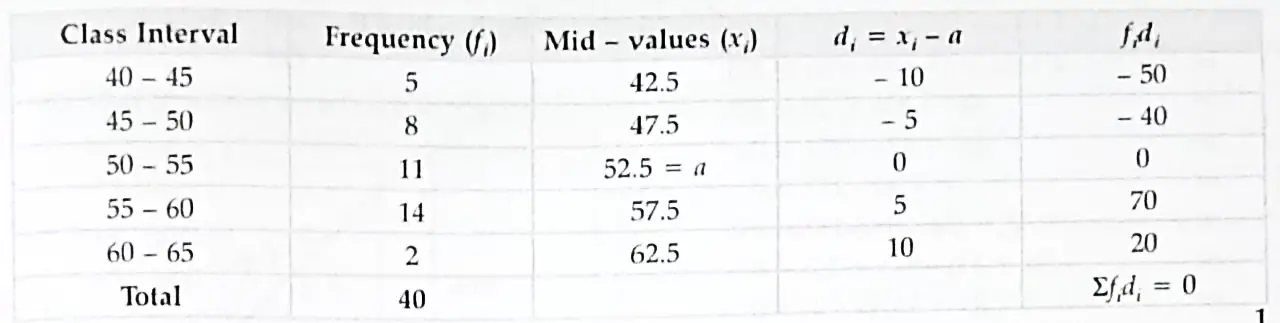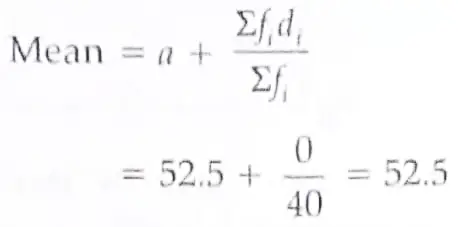         1

         1

4. (a) There are three measures of central tendency

Mean, Median and mode          1

(b) According to the empirical relationship between mean, median and mode..

2 Mean = 3 Median – Mode

or Mode = 3 Median – 2 Mean

= 3(138.57) – 2(145.20)

= 415.71 – 290.40

= 125.31          1

5. Let two parts be x and 27 – x.

The sum of reciprocals of both parts = 3/20

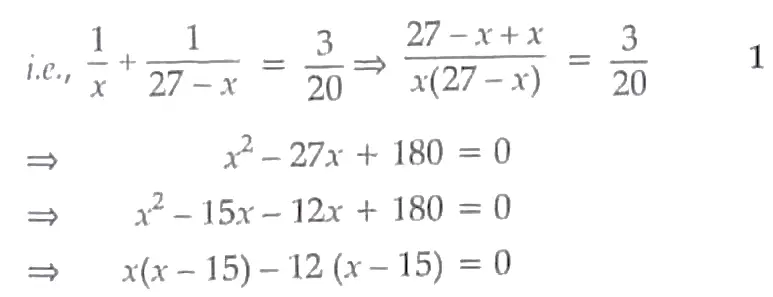
⇒ (x-15) (x – 12) = 0          1

⇒ x = 12 or 15.

Hence, The two parts are 12 and 15.          1

6. Let ‘L’ be the length of string

From the figure, BC = 108 m, ∠A = 60°

∠B = 90°

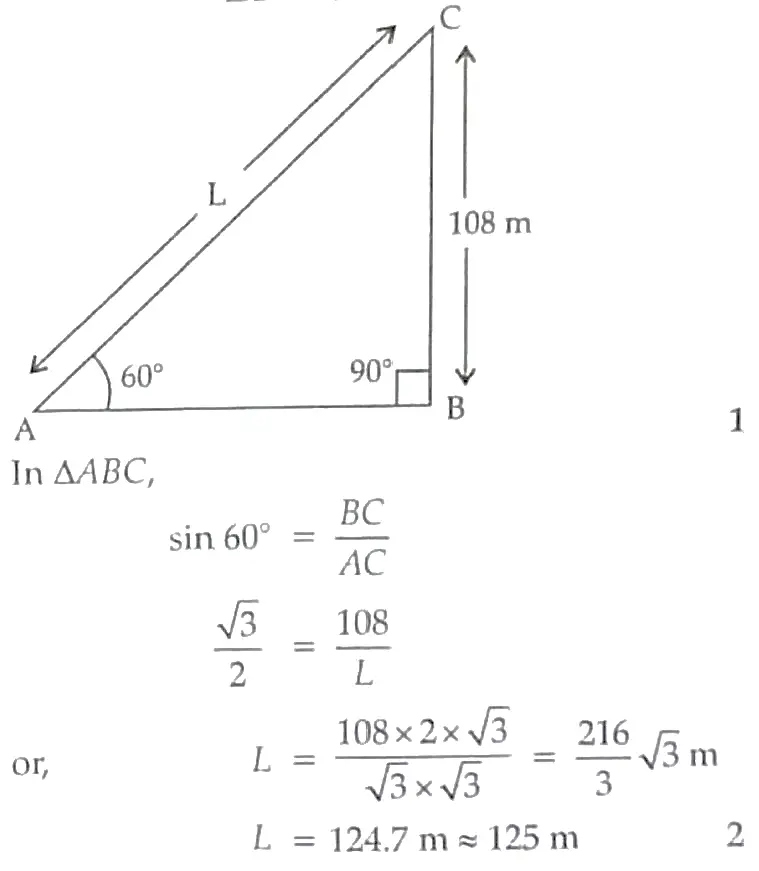
Section – B

7. Given, first term, a = 5 and last term, l = a_n = 45        ½

Given given, sum S_n = 400

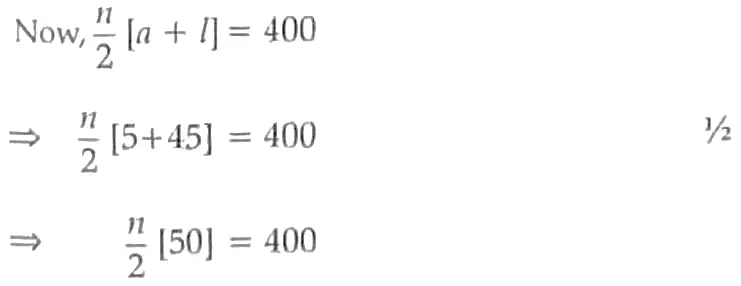
So, n = 16         1

Now, n^th terms of an A.P.,

a_n = a + (n − 1)d

45 = 5 + (16 – 1)d

40 = 15d

⇒ d = 8/3        1

Hence, the number of terms and common difference are 16 and 8/3.

8. Let first odd integer = x

second odd integer = x + 2 and

third odd integer = x + 4

According to the question,

(x)² + (x + 2)² + (x + 4)² = 371         1

or x² + x² + 4 + 4x + x² + 16 + 8x = 371

or 3x² + 12x + 20 = 371

or 3x² + 12x – 351 = 0

or x² + 4x – 117 = 0         1

or x² + 13x – 9x – 117 = 0

or x(x +13) – 9 (x + 13) = 0

or (x + 13) (x – 9) = 0

or x = -13

or x = 9

∴ x is odd positive integer so – 13 is rejected.

Therefore, the numbers are 9, 11, 13.         1

9. A vertical tower is surmounted by flag staff.

Distance between observer and the tower DC = 90

Therefore, the height of tower is 51.96 m and the height of flag staff = 38.04 m.          1

OR

Height of the electric pole = 21 m = AB

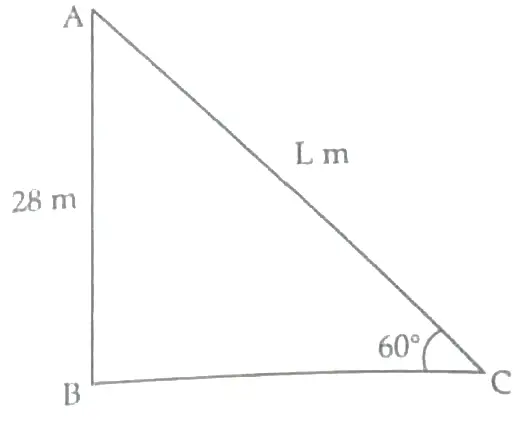            1

The angle made by steel wire with ground (horizontal) θ = 60°

Let length of wire = L = AC

So, from the figure formed we have ABC as a right triangle.

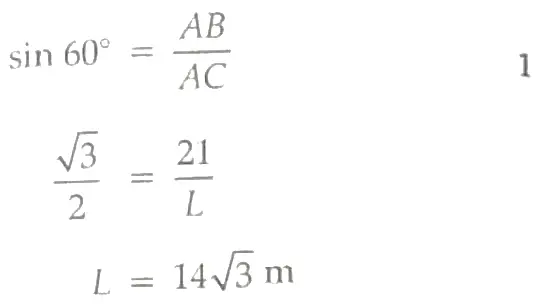
Hence, Length of the wire (L) = 14√3 m.         1

10.

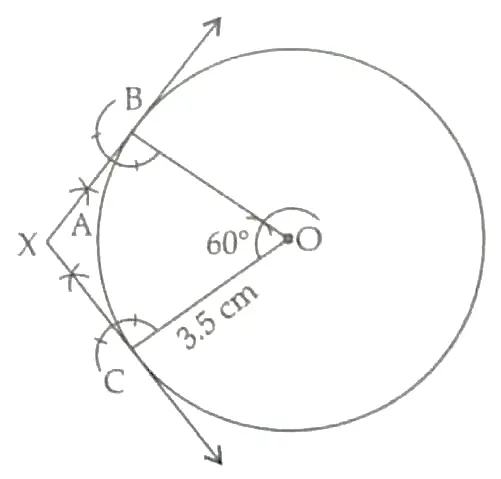        2

Steps of construction:

1. Draw a circle with centre O and radius 3.5 cm.

2. Draw any radius OC.

3. Construct ∠COB = 180° – 120° = 60°

4. Draw XB ⊥ OB and CX ⊥ OC

5. Thus XB and XC are the required tangents which are intersecting at X at an angle of 120°.         1

Section – C

11.

Substituting the value of x in equation (i),

y = 24 – 9 = 15

Hence, x = 9 and y = 15.           1

OR

= 40 + 4.70

= 44.70           2

12. Given : A rectangle ABCD circumscribe a circle which touches the circle at P, Q, R, S.

To Prove: ABCD is a square.

Proof: As tangents from external point are equal.

AP = AS     …(1)          ½

PB = BQ     …(2)           ½

DR = DS     …(3)           ½

RC = QC      …(4)           ½

Adding eq. (1), (2), (3) and (4), we get

On AP + PB + DR + RC = AS + BQ + DS + QC

AB + CD = AD + BC

2AB = 2BC            1

[Opposite sides of a rectangle are equal]

∴ AB = BC

Tense, adjacent sides are equal so ABCD is a square.

            1

Case Study – 1

13. (i) For cuboid,

Length = 12 cm, breadth = 8 cm and height = 4.5 cm

∴ Volume of cuboid = Length x Breadth

= 12 x 8 x 4.5

= 432 cm³.           1

(ii) For conical depression,

Radius, (r) = 0.6 cm

And Depth (h) = 2.1 cm

∴ Volume of conical depression

= (1/3)πr²h          1

= 1/3 x 22/7 x 0.6 x 0.6 x 2.1

= 0.792 cm³          1

Case Study – 2

14. (i) In right triangle ABC,

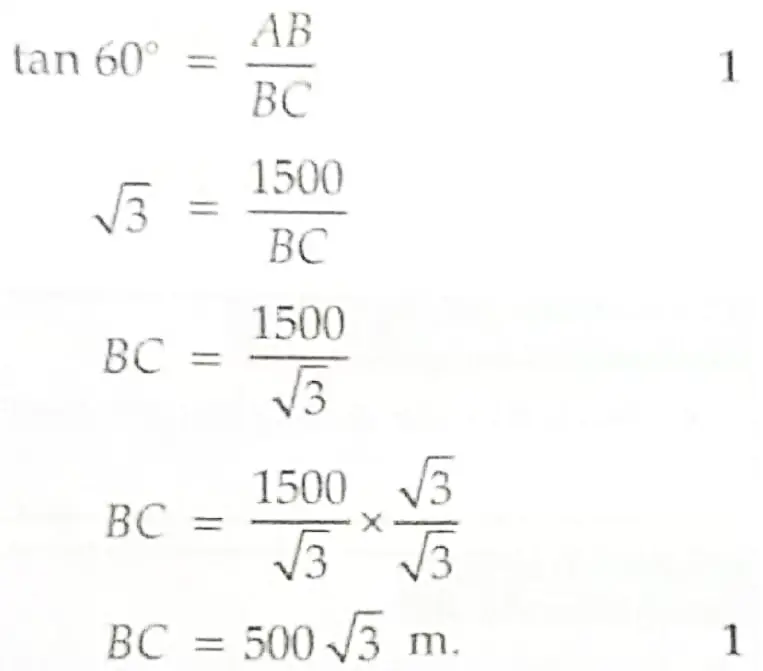
(ii) Height at which plane is flying AB = 750 m

and BC = 500 √3 m [From part (i)]

In △ABC, ∠B = 90°