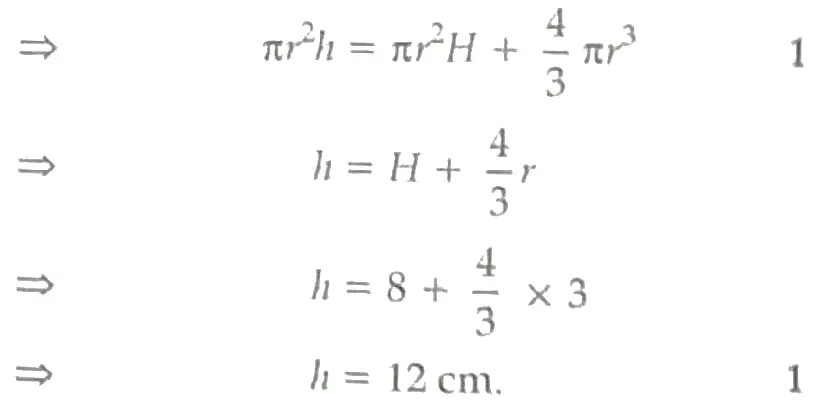Maths Basic Term 2 Sample Paper 2022 (Solved)

Class 10 Maths Basic Term 2 Sample Paper 2022, (Maths) exams are Students are taught thru NCERT books in some of the state board and CBSE Schools. As the chapter involves an end, there is an exercise provided to assist students to prepare for evaluation. Students need to clear up those exercises very well because the questions inside the very last asked from those.

Sometimes, students get stuck inside the exercises and are not able to clear up all of the questions. To assist students, solve all of the questions, and maintain their studies without a doubt, we have provided a step-by-step NCERT Sample Question Papers for the students for all classes. These answers will similarly help students in scoring better marks with the assist of properly illustrated Notes as a way to similarly assist the students and answer the questions right.

Class 10 Maths Basic Term 2 Sample Paper 2022

General Instructions:

1. The question paper consists of 14 questions divided into 3 sections A, B, C.

2. Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.

3. Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.

4. Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study based questions.

 

Section – A

[ 2 Marks Each ]

1. Find the roots of the quadratic equation 3x² – 7x – 6 = 0.

OR

Find the values of k for which the quadratic equation 3x² + kx + 3 = 0 has real and equal roots.

2. Three cubes each of volume 64 cm³ are joined end to end to form a cuboid. Find the total surface area of the cuboid so formed?

3. An inter house cricket match was organized by a school. Distribution of the runs made by the students is given below. Find the median runs scored.

Runs Scored	0 – 20	20 – 40	40 – 60	60 – 80	80 – 100
Number of students	4	6	5	3	4

4. Find the common difference of the A. P. 4, 9, 14, … If the first term changes to 6 and the common difference remains the same then write the new AP.

5. The mode of the following frequency distribution is 38. Find the value of x.

Class Interval	0-10	10 – 20	20 – 30	30 – 40	40 – 50	50 – 60	60 – 70
Frequency	7	9	12	16	x	6	11

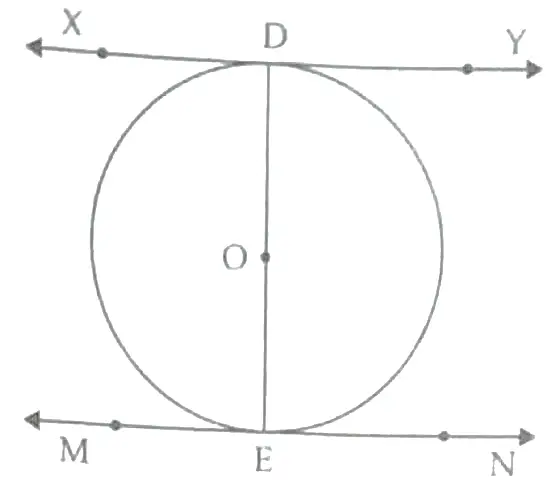
6. XY and MN are the tangents drawn al the end points of the diameter DE of the circle with centre O. Prove that XY || MN.

OR

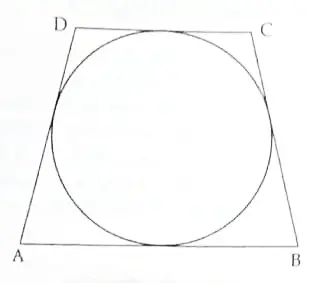
In the given figure, a circle is inscribed in the quadrilateral ABCD. Given AB = 6 cm, BC = 7cm and CD = 4 cm. Find AD.

 

Section – B

[ 3 Marks Each ]

7. An A.P. 5, 8, 11 … has 40 terms. Find the last term. Also find the sum of the last 10 terms.

8. A tree is broken due to the storm in such a way that the top of the tree touches the ground and makes an angle of 30° with the ground. Length of the broken upper part of the tree is 8 meters. Find the height of the tree before it was broken.

OR

Two poles of equal height are standing opposite each other on either side of the road 80 m wide. From a point between them on the road the angles of elevation of the top of the two poles are respectively 60° and 30°. Find the distance of the point from the two poles.

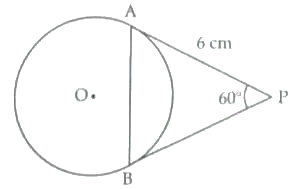
9. PA and PB are the tangents drawn to a circle with centre O. If PA = 6 cm and ∠APB = 60° , then find the length of the chord AB.

10. The sum of the squares of three positive numbers that are consecutive multiples of 5 is 725. Find the three numbers.

 

Section – C

[4 Marks each]

11. Construct two concentric circles of radii 3 cm and 7 cm. Draw two tangents to the smaller circle from a point P which lies on the bigger circle.

OR

Draw a pair of tangents to a circle of radius 6 cm which are inclined to each other at an angle of 60°. Also find the length of the tangent.

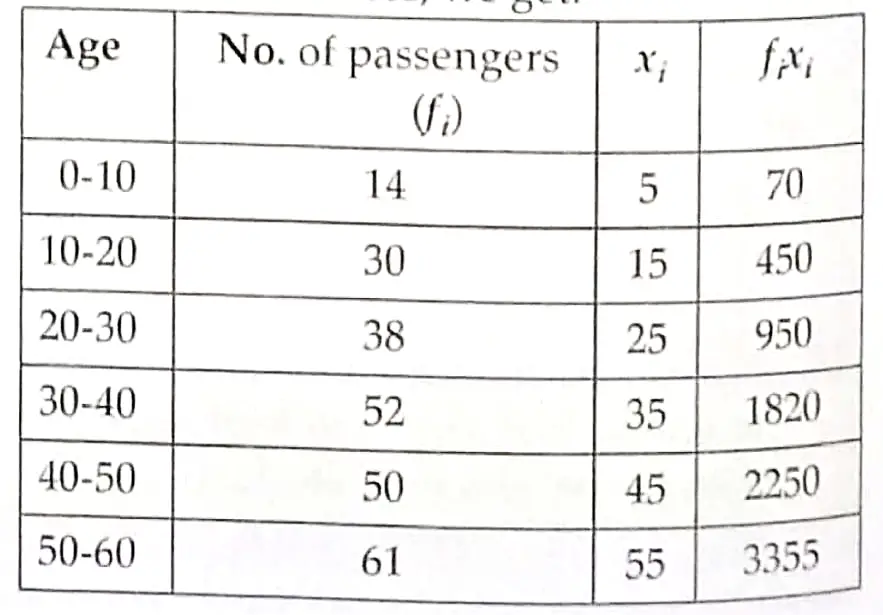
12. The following age wise chart of 300 passengers flying from Delhi to Pune is prepared by the Airlines staff:

Age	Less than 10	Less than 20	Less than 30	Less than 40	Less than 50	Less than 60	Less than 70	Less than 80
Number of Passengers	14	44	82	134	184	245	287	300

Find the mean age of the passengers.

 

Case Study – 1

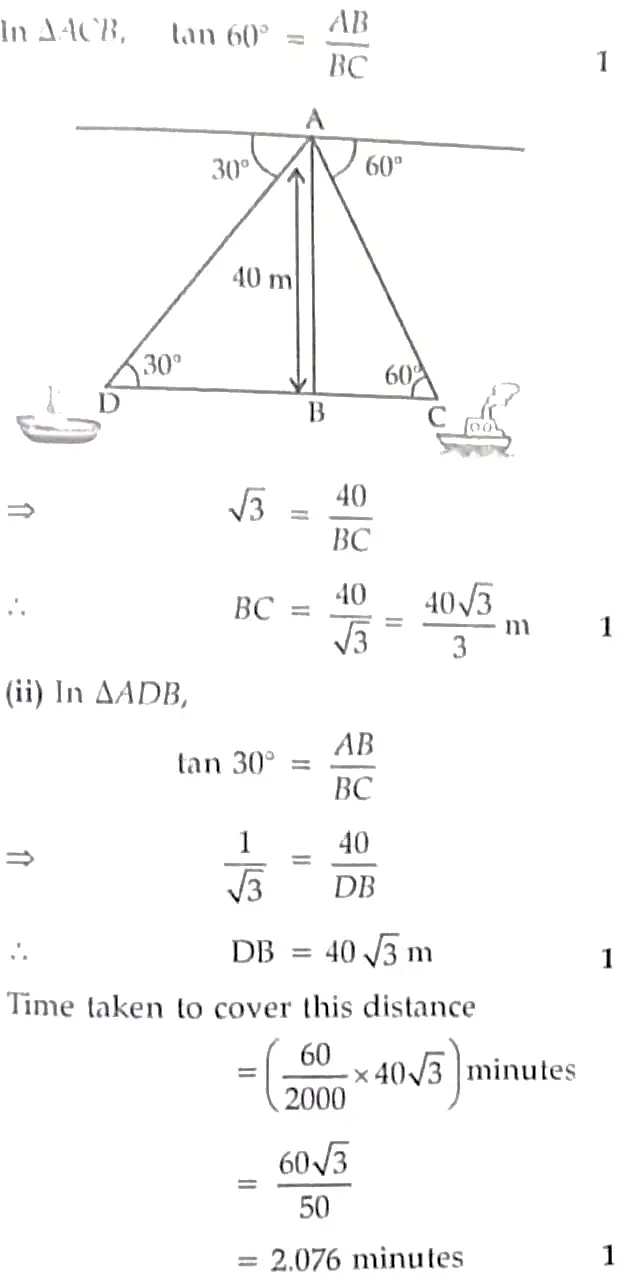
13. A lighthouse is a tall tower with light near the top. These are often built on islands, coasts or on cliffs. Lighthouses on water surface act as a navigational aid to the mariners and send warning to boats and ships for dangers. Initially wood, coal would be used as illuminators. Gradually it was replaced by candles, lanterns, electric lights. Now a days they are run by machines and remote monitoring.

Prongs Reef lighthouse of Mumbai was constructed in 1874 – 75. It is approximately 40 meters high and its beam can be seen at a distance of 30 kilometres. A ship and a boat are coming towards the lighthouse from opposite directions. Angles of depression of flash light from the lighthouse to the boat and the ship are 30° and 60° respectively.

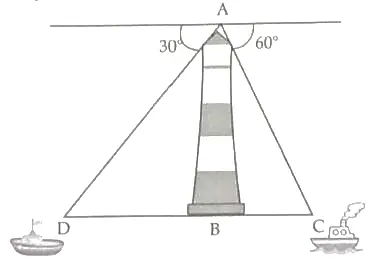
(i) Which of the two, boat or the ship is nearer to the light house. Find its distance from the lighthouse?          [2]

(ii) Find the time taken by the boat to reach the light house if it is moving at the rate of 2 km per hour.                [2]

 

Case Study – 2

14. Krishnanagar is a small town in Nadia District of West Bengal. Krishnanagar clay dolls are unique in their realism and quality of their finish. They are created by modelling coils of clay over a metal frame. The figures are painted in natural colours and their hair is made either by sheep’s wool or jute. Artisans make models starting from fruits, animals, God, goddess, farmer, fisherman, weavers to Donald Duck and present comic characters. These creations are displayed in different national and international museums.

Here are a few images (not to scale) of some clay dolls of Krishnanagar.

The ratio of diameters of red spherical apples in Doll-1 to that of spherical oranges in Doll-2 is 2 : 3. In Doll-3, male doll of blue colour has cylindrical body and a spherical head. The spherical head touches the cylindrical body. The radius of both the spherical head and the cylindrical body is 3 cm and the height of the cylindrical body is 8 cm. Based on the above information answer the following questions:

(i) What is the ratio of the surface areas of red spherical apples in Doll-1 to that of spherical oranges in Doll-2 ?         [2]

(ii) The blue doll of Doll-3 is melted and its clay is used to make the cylindrical drum of Doll-4. If the radius of the drum Is also 3 cm, find the height of the drum.          [2]

 

Solution of Sample Paper

 

Section – A

1. 3x² – 7x – 6 = 0

⇒ 3x² – 9x + 2x – 6 = 0                 ½

⇒ 3x(x – 3) + 2(x – 3) = 0

⇒ (x – 3)(3x + 2) = 0              ½

∴ x = 3, –⅔                  1

Detailed Solution:

3x²– 7x – 6 = 0 (Given)

Using splitting middle term method,

3x² – 9x + 2x – 6 = 0              ½

⇒ 3x(x – 3) + 2(x – 3) = 0

⇒ (3x + 2) (x – 3) = 0            ½

Either 3x + 2 = 0

⇒ x = –⅔

or x – 3 = 0

or x = 3

Hence, 3 or –⅔ are the roots of the quadratic equation.          1

OR

Since the roots are real and equal,

 ∴ D = b² – 4ac = 0

⇒ k² – 4 × 3 × 3 = 0 (∴ a = 3, b = k, c = 3)         1

⇒ k² = 36

⇒ k = 6 or -6              ½ + ½

Detailed Solution:

Given: 3x² + kx + 3 = 0

On comparing it with ax² + bx + c = 0

a = 3, b = k, c = 3            1

Since, roots are real and equal.

⇒ Discriminant = 0

or b² – 4ac = 0

or (k)² – 4(3) (3) = 0

or k² – 36 = 0

or k² = 36

or k = ±6

i.e., k = 6 or -6                ½ + ½

2. Let l be the side of the cube and L, B, H be the dimensions of the cuboid

Since l³ = 64 cm³

 ∴ l = 4 cm            ½

Total surface area of cuboid = 2[LB + BH + HL],

Where L = 12 cm, B = 4 cm and H = 4 cm              ½

= 2(12 × 4 + 4 × 4 + 4 × 12) cm²

= 224 cm²                  1

3.

Runs Scored	Frequency	Cumulative Frequency
0 – 20	4	4
20 – 40	6	10
40 – 60	5	15
60 – 80	3	18
80 – 100	4	22

  ½

Total frequency (N) = 22

N/2 = 11;              ½

So 40 – 60 is the median class

                                                                           ½

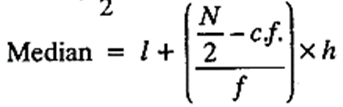
= 40 + (11 – 10)/5 × 20

= 44 runs                ½

4. The common difference is

9 – 4 = 5          1

If the first term is 6 and common difference is 5, then new AP is, 6,6 + 5,6 + 10…..

= 6,11,16….           1

Detailed Solution:

Since 4, 9, 14. ….. is given in A.P.

⇒ a = 4,

d = 2^nd term – 1^st term

d = 9 – 4 = 5

Common difference of the given A.P. is 5.           1

If first term is 6 and common difference = 5

i.e., a₁ = 6

a₂ = a + d = 6 + 5 = 11

a₃ = a + 2d = 6 + 2(5) = 16

∴ New A.P. will be 6, 11, 16…            1

5. ∵ Mode = 38.

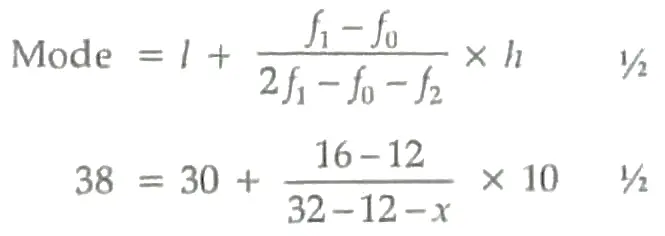
∴ The modal class is 30 – 40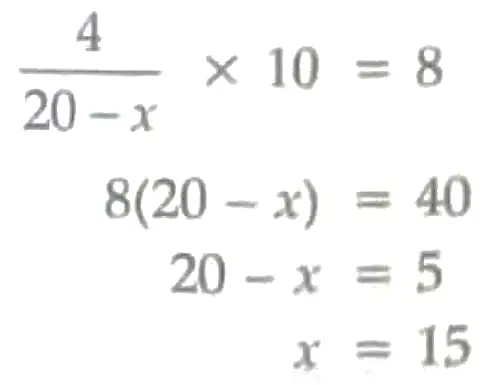.               ½

           ½

6.

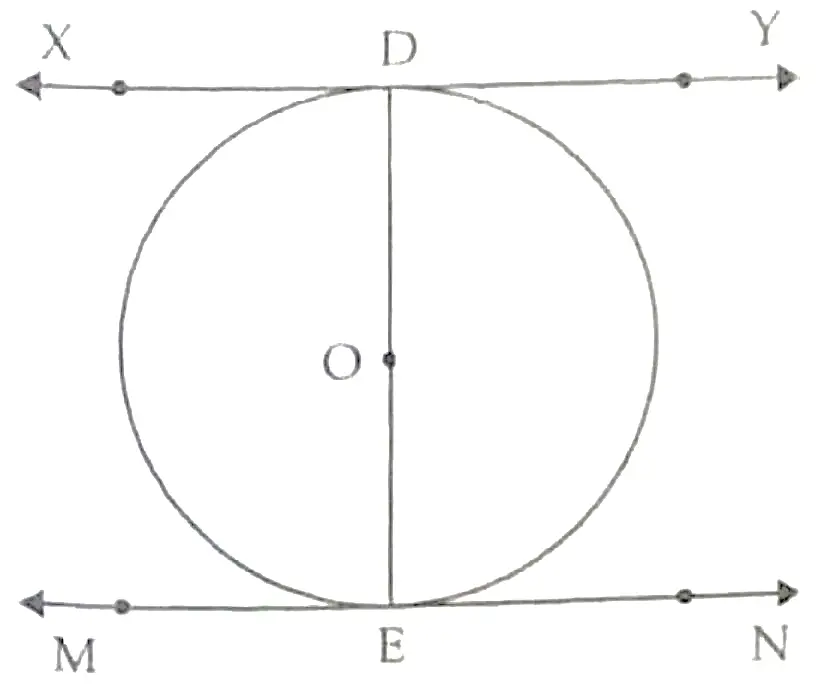
∵ XY is the tangent to the circle at the point D

∴ OD ⊥ XY

⇒ ∠ODX = 90°

⇒ ∠EDX = 90°          ½

Also, MN is the tangent to the circle at E

∴ OE ⊥ MN

⇒ ∠OEN = 90°

⇒ ∠DEN = 90°

⇒ ∠EDX = ∠DEN (each 90°).            ½

which are alternate interior angles.

∴ XY || MN          1

Detailed Solution:

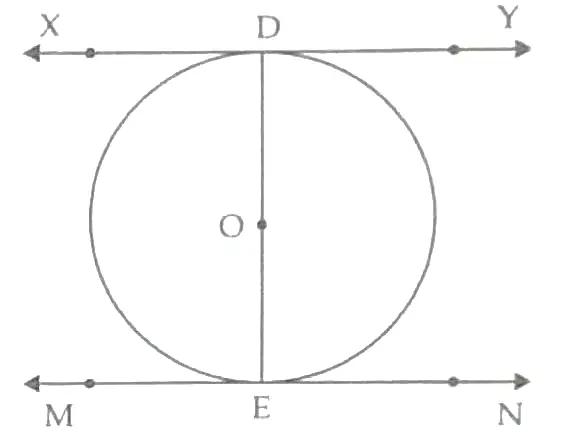
Given: DE is a diameter of the circle with centre O. XY and MN are tangents to the circle at D and E.

To Prove: XY || MN.

Proof: According to the theorems, Radius is always perpendicular to the tangent at point of contact.

⇒ OD ⊥ XY [OD is the Radius and XY is the tangent]

i.e., ∠ODX = ∠ODY = 90°.           ½

Similarly, if OE is the radius and MN is the tangent, then

OE ⊥ MN

i.e., ∠OEN = ∠OEM = 90°              ½

∵ ∠ODX = ∠OEN = 90° (Alternate Angles)

Hence, XY || MN.

Proved                 1

OR

∵ Tangent segments drawn from an external point to a circle are equal

∴ BP = BQ, CR = CQ, DR = DS, AP = AS

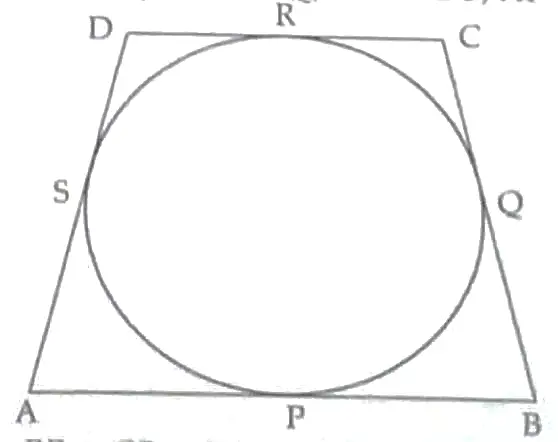
⇒ BP + CR + DR + AP = BQ + CQ + DS + AS               1

⇒ AB + DC = BC + AD

AD = 10 – 7 = 3 cm            1

 

Section – B

7. First term of the A.P. (a) = 5

Common difference (d) = 8 – 5 = 3

Last term = a₄₀

= a + (40 – 1)d

= 5 + 39 x 3 = 122         1

Also a₃₁ = a + 30d

= 5 + 30 x 3 = 95              1

Sum of last 10 terms

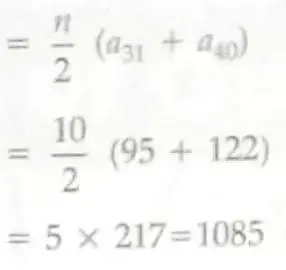              1

Detailed Solution:

5, 8, 11, … is given in A.P. which has 40 terms.

So, first term a = 5,

and common difference d = 8 – 5 = 3

Total terms n = 40

Let the last term be n^th term,

a = a + (n – 1)d

∴ a₄₀ = 5 + (40 – 1)3

⇒ a₄₀ = 5 + (39)3

⇒ a₄₀ = 5 + 117

⇒ a₄₀ = 122               1

Now, a₃₁ = 5 + (31 – 1)3

= 5 + (30)3

= 5 + 90

= 95               1

For last 10 terms,

First term, a’ = a₃₁ = 95

Last term, l’ = a₄₀ = 122

∴ Sum of last 10 terms

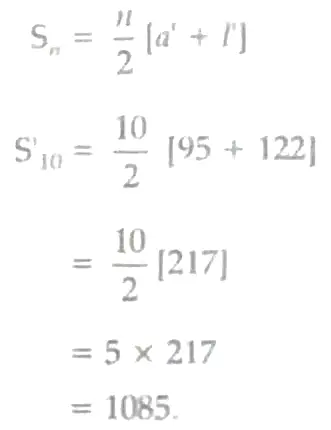1

8.

OR

Let AB and CD be two poles of height h meters also let P be a point between them on the road which is x meters away from foot of first pole AB, PD = (80 – x) meters.

9. PA = PB (tangents drawn to a circle from an external point are equal)

∴ In △APB, ∠PAB = ∠PBA

Also, ∠APB = 60°         1

In △APB,

∵ sum of three angles is 180°

∠PAB + ∠PBA = 180° – ∠APB

180° – 60° = 120°.

∵ ∠PAB = ∠PBA = 60° ( ∠PAB = ∠PBA)          1

∴ △APB is an equilateral triangle.

Hence, AB= 6 cm.        1

Detailed Solution:

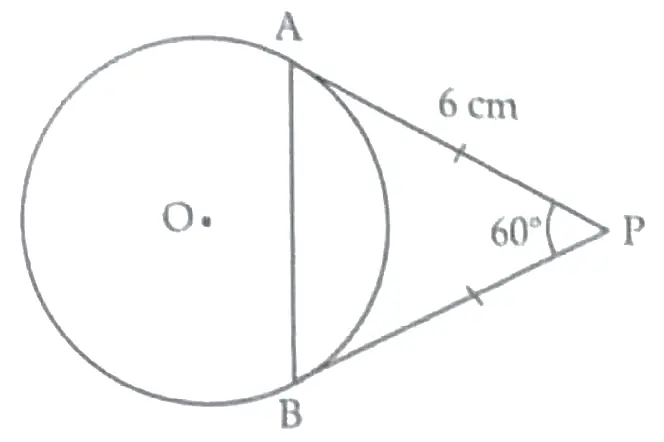
It is given that PA = 6 cm and ∠APB = 60°

According to the property that tangents drawn from same external point are equal in length.

∴ PA = PB = 6 cm.           1

⇒ ∠PAB = ∠PBA [Equal sides have equal opposite angles]

In △APB,

According to angle sum property of a triangle.

∠PAB + ∠PBA + ∠APB = 180°

∠PAB + ∠PAB + 60° = 180°

2∠PAB = 180° – 60°

∠PAB = 120°/2 = 60°

∴ ∠APB = ∠PAB            1

= ∠PAB = 60°

So, △APB is an equilateral triangle. In an equitation triangle all sides are equal.

∴ AB = PA = PB = 6 cm

or AB = 6 cm.         1

10. Let the three consecutive multiples of 5 be 5x, 5x + 5, 5x + 10.

Their squares are (5x), (5x + 5)² and (5x + 10).

(5x)² + (5x + 5)² + (5x + 10)² = 725           1

⇒ 25x² + 25x² + 50x + 25 + 25x + 100x + 100 = 725

⇒ 75x² + 150x – 600 = 0

⇒ x² + 2x – 8 = 0

⇒ (x + 4) (x – 2) = 0

⇒ x = -4, 2

⇒ x = 2 (ignoring-ve value)               1

So the numbers are 10, 15 and 20.          1

Detailed Solution:

Let first consecutive number = 5x

Second number = 5(x + 1) = 5x + 5

Third number = 5(x + 2) = 5x + 10

According to the question,

(5x)² + (5x + 5)² + (5x + 10)² = 725          1

⇒ 25x² + 25x² + 25 + 50x + 25x² + 100 + 100x =725

⇒ 75x² + 150x + 125 – 725 = 0

⇒ 75(x² + 2x – 8) = 0

or x² + 2x – 8 = 0

x² + 4x – 2x – 8 = 0

⇒ x(x + 4) -2(x + 4) = 0

⇒ (x – 2)(x + 4) = 0

either x – 2 = 0

⇒ x = 2

or x + 4 = 0

x = -4 (ignoring -ve value)         1

1^st number = 5x = 5(2) = 10

2^nd number = 5x + 5 = 5(2) + 5 = 15

3^rd number = 5x + 10

= 5(2) + 10 = 20           1

 

Section – C

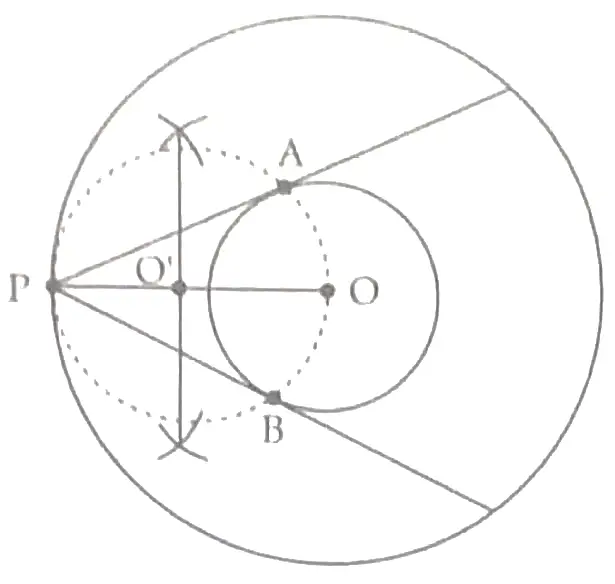
11. Draw two concentric circles with center O and radii 3 cm and 7 cm respectively.              1

Join OP and bisect it at O’,

so PO’ = O’O           1

Construct circle with center O’ and radius O’O           1

Join PA and PB.          1

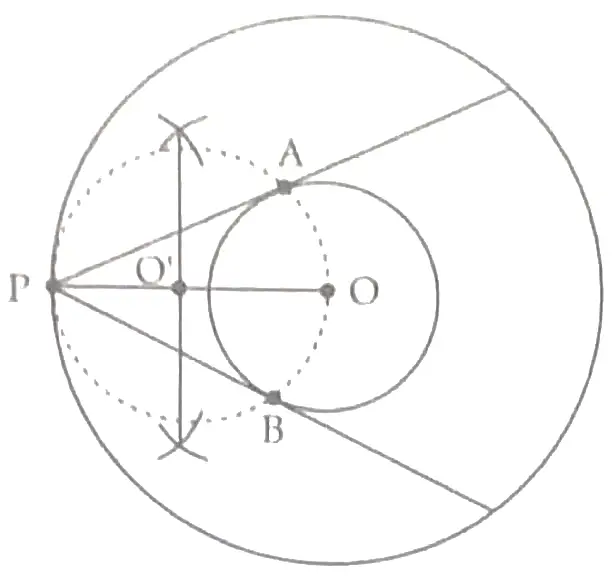
Detailed Solution:

                 3

Steps of construction:

(i) Draw two concentric circles of radii 3 cm and 7 cm respectively.

(ii) Make a point P on the outer circle and join OP.

(iii) Draw perpendicular bisector of OP. Let it intersect OP at O’.

(iv) With O’ as centre and O’O as radius draw a circle and it should pass through P.

(v) Let this circle intersect inner circle at A and B.

(vi) Join PA and PB. Thus PA and PB are required tangents.         1

OR

Draw a circle of radius 6 cm

Draw OA and construct ∠ AOB = 120°         1

Draw ∠OAP = ∠OBP = 90°            1

PA and PB are required tangents          1

Join OP and apply

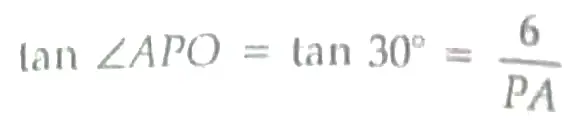
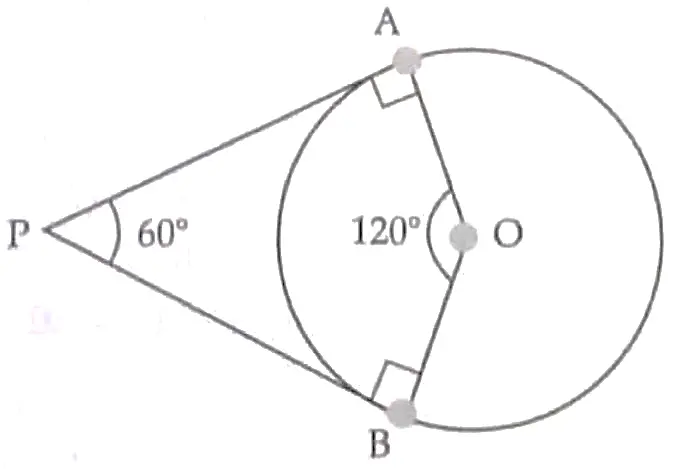
⇒ Length of tangent = 6√3 cm              1

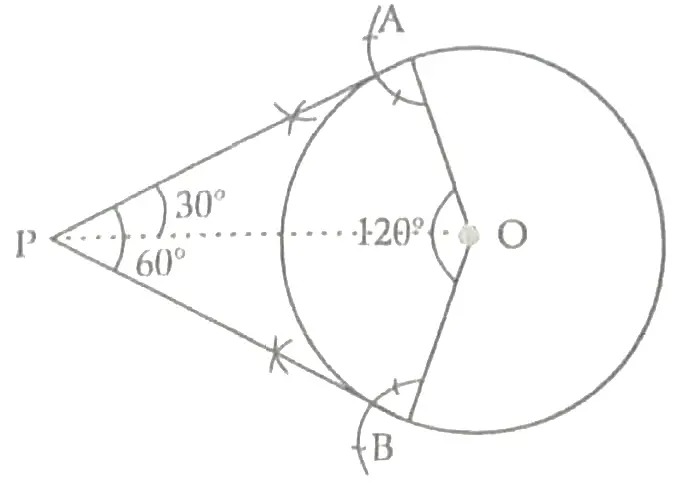
Detailed Solution:

           2

Steps of construction:

(i) Draw a circle of radius 6 cm with centre O.

(ii) Draw any radius OA and make an angle of 180° – 60° = 120° at O such that ∠AOB = 120°.

(iii) Draw AP ⊥ OA and BP ⊥ OB. Let the two perpendiculars meet at point P.

(iv) Thus PA and PB are the required tangents to the given circle inclined at angle of 60⁰.

(v) Join OP

∵ Tangents are equally is clined to each other.

∴ ∠OPA = ∠OPB = 30°

In right angle △OAP,

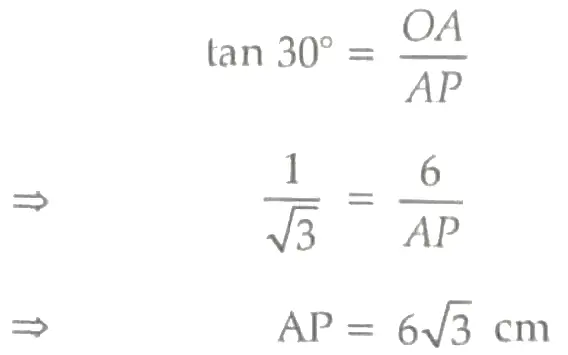           2

Hence, the length of the tangent is 6√3 cm.

12. Converting the cumulative frequency table into exclusive classes, we get:

 

Case Study – 1

13. (i) The ship is nearer to the lighthouse as its angle of depression is greater.

Detailed Solution:

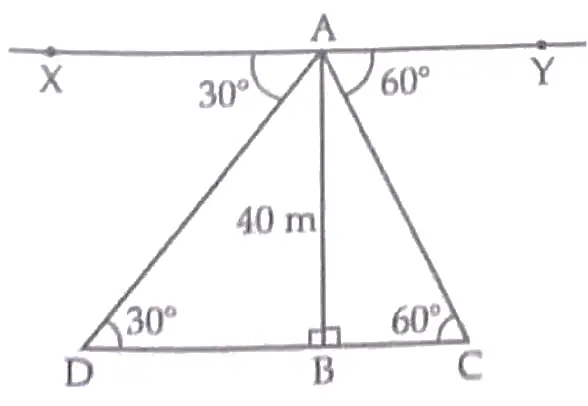
Let AB is the height of the lighthouse

i.e., AB = 40 m

∠XAD= ∠ADB = 30° [ ∵ Angle of depression = Angle of elevation]

Similarly,

∠YAC = ∠ACB = 60°

The ship is nearer to the lighthouse as its angle of depression is greater.           1

 

Case Study – 2

14. (i) Let r₁ and r₂ be respectively the radii of apples and oranges

∴ 2r₁ : 2r₂ = 2 : 3

⇒ r₁ : r₂ = 2 : 3 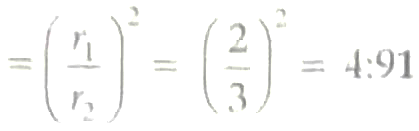        ½

            ½

(ii) Let the height of the drum be h.

Volume of the drum = volume of the cylinder + volume of the sphere

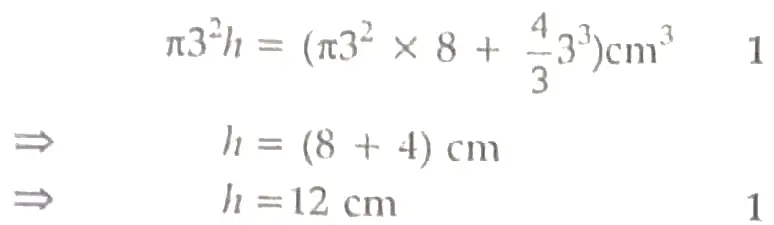
Detailed Solution:

(i) Let r₁ and r₂ be the radii of apples and oranges respectively.

According to the question,

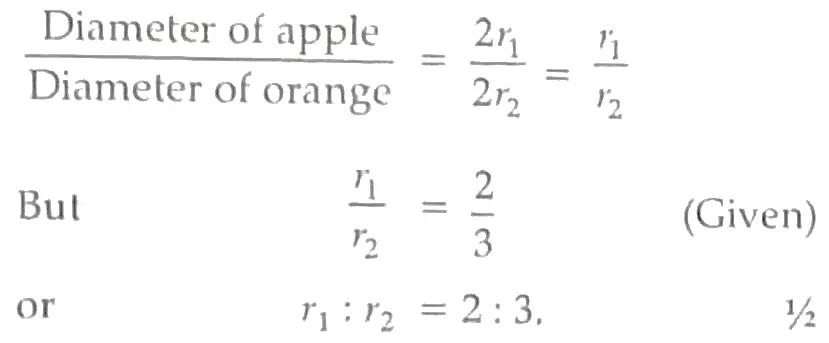
Total surface Area of sphere = 4πr²

Detailed Solution:

(ii) Let the drum of height be h cm.

⇒ Radius of cylindrical part in doll-3 = 3 cm

Radius of cylindrical drum in doll-4 = 3 cm

Radius of spherical part in doll-3 = 3 cm

Height of cylindrical part in doll-3 = 8 cm (H)

Blue doll of doll-3 is melted and remade into a cylindrical doll-4.

⇒ Volume of the cylindrical drum for doll-4 = Volume of cylindrical part + volume of serpent in doll-3